【入門編】アルゴリズムとデータ構造とは？図でわかりやすく解説

アルゴリズムとデータ構造は、効率的なプログラムの処理を考えたり、大量のデータをスムーズに管理したりするために必要な知識です。しかし、独特な考え方が必要であるため、エンジニアの中にも苦手意識を持つ人が多い分野です。

この記事では、アルゴリズムとデータ構造についての基本について、図を用いてわかりやすく解説します。

アルゴリズムとデータ構造とは何か？初心者向けに解説

「アルゴリズム」とは、算法とも呼ばれ、コンピューターが問題を解決する際に沿う手順のことです。一方、「データ構造」とは、データを扱いやすくするために一定の形式に当てはめて格納された、データの集合体のことで、データを効率的に管理するための整理方法ともいえます。

プログラミング経験があるエンジニアであれば、「配列」という言葉を知っている方も多いのではないでしょうか。この配列も、データ構造の一種です。

理解を容易にするために、料理を例に挙げてアルゴリズムとデータ構造を考えてみましょう。料理には具材が必要です。そして、料理を完成させるためには、レシピの手順に沿って調理をしなければなりません。これをアルゴリズムとデータ構造に置き換えると、具材がデータ構造、そして料理する工程がアルゴリズムになります。

具材＝データ構造
料理工程＝アルゴリズム

これと同じように、プログラムにおいても、両者は切っても切り離すことができない存在です。

アルゴリズムとデータ構造を学ぶと何がわかる？

アルゴリズムやデータ構造について学ぶと、どのようなメリットがあるのでしょうか。

1つ目は、最適なアルゴリズムを使い分けることができる点です。例えば、データを並び替えるソートには複数の種類がありますが、アルゴリズムを理解していれば、最適なソートアルゴリズムをプログラムの中に採用できるようになります。

2つ目は、わかりやすいコードの作成および、共有がしやすくなることです。基本を理解することで、整理された美しいコードを書くことができるようになるため、ほかのエンジニアにコードを理解してもらいやすくなります。

3つ目は、問題解決に役立つという点です。プログラミングにおいて問題が発生したとき、アルゴリズムやデータ構造といった基本を理解していれば、仕組みを考え、素早く解決策を見つけ出すことができるようになります。そのため、エラー処理が速くなったり、問題に対して柔軟に対処ができるようになったりというメリットが考えられます。

　

アルゴリズムの基本をわかりやすく解説

ここからは、アルゴリズムの基本である探索、整列、再帰的アルゴリズムについてわかりやすく解説します。

サーチ（探索）アルゴリズム

「サーチ(探索)アルゴリズム」とは、膨大のデータの中から目的のデータを探し出すことができるアルゴリズムのことです。例えば、検索エンジンにおいて、ユーザーが知りたい情報を提供するためにサーチアルゴリズムが採用されています。また、SNSサービスにおいても、ユーザーに必要な情報を選別して提供するために活用されているのです。

サーチアルゴリズムには、リニアサーチ（線形探索法）とバイナリサーチ（二分探索）という2つの考え方があります。

リニアサーチ

リニアサーチは、線形探索法と呼ばれ、データ群の端から目的の情報があるかどうか探索していくやり方です。

探索方法としてはとてもシンプルで、端から順番に、目的の情報であるかどうか一つひとつ探索します。

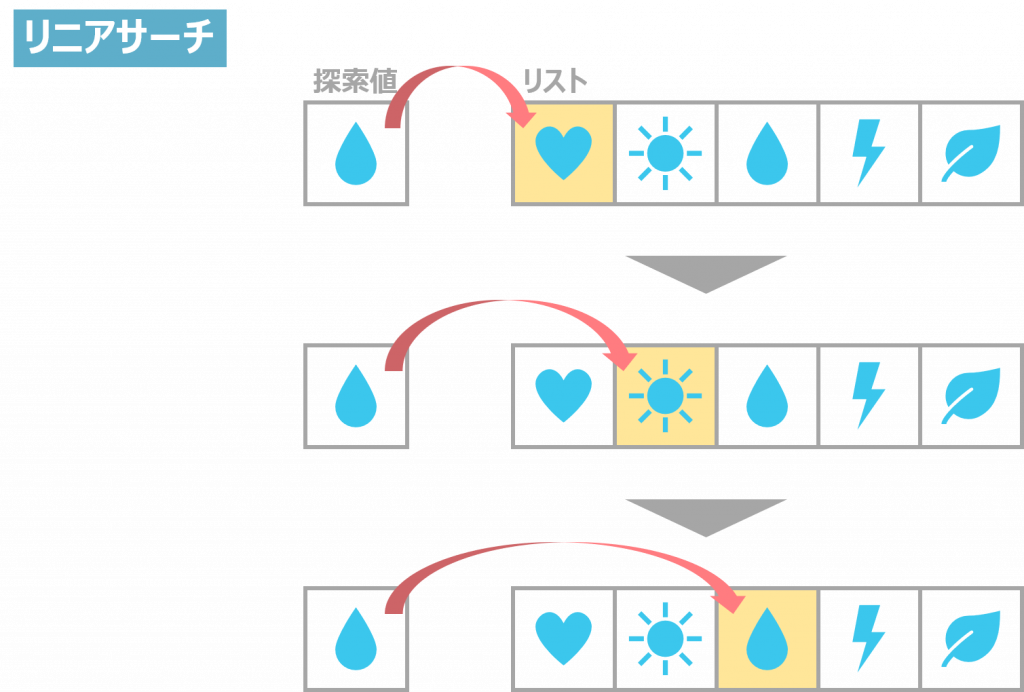
実際にC言語でリニアサーチをプログラミングすると、下記のようになります。

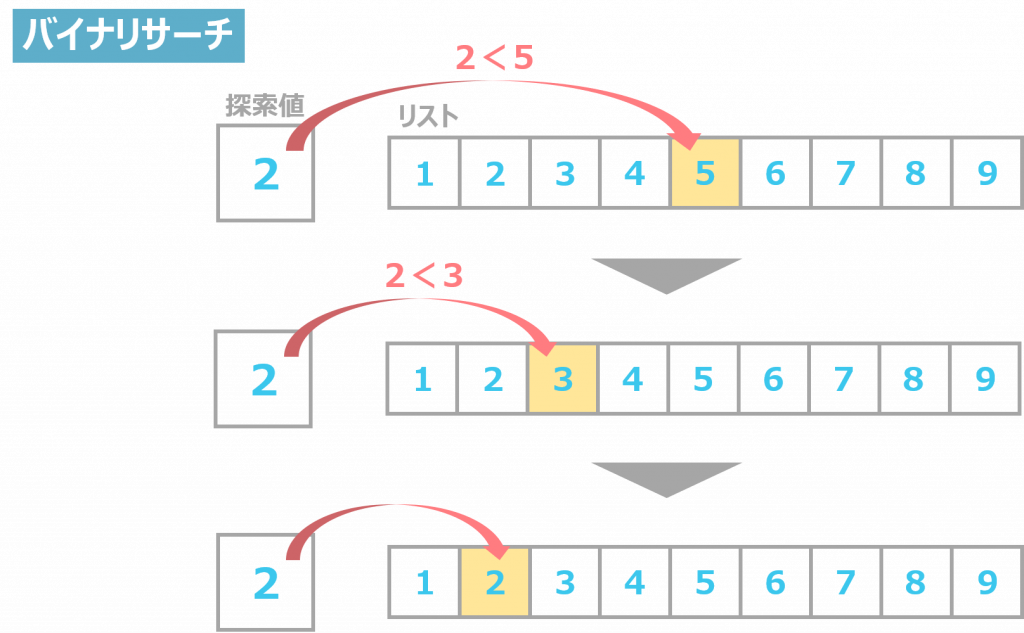
バイナリサーチ

一方、バイナリサーチは、データ群にある数字が目的の数字よりも大きいか小さいかに分けて、探索をしていく方法です。

ただし、バイナリサーチが使えるのは、データ群に規則性がある場合に限ります。

ソート（整列）アルゴリズム

「ソート(整列)アルゴリズム」とは、一定の規則に従って大量のデータを並べ替えるアルゴリズムのことです。ソートアルゴリズムには、全部で7種類の考え方があります。

バブルソート

1つ目がバブルソートです。バブルソートでは、隣同士の値を比較して、何度も入れ替えを行うことで、データを降順や昇順に並べ替えることができます。

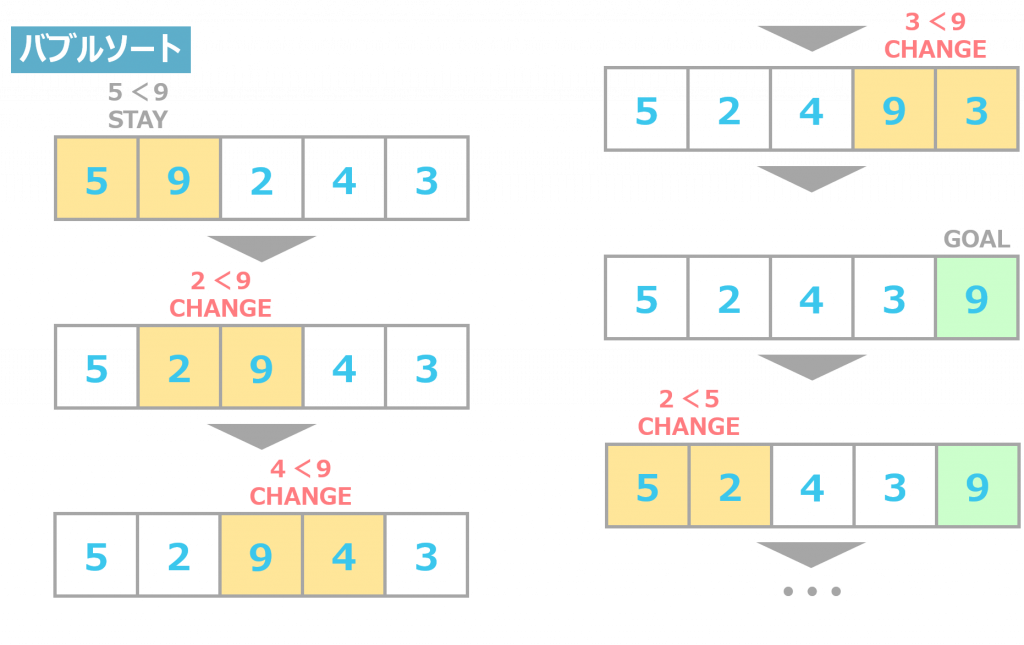
C言語でのコードは下記の通りです。

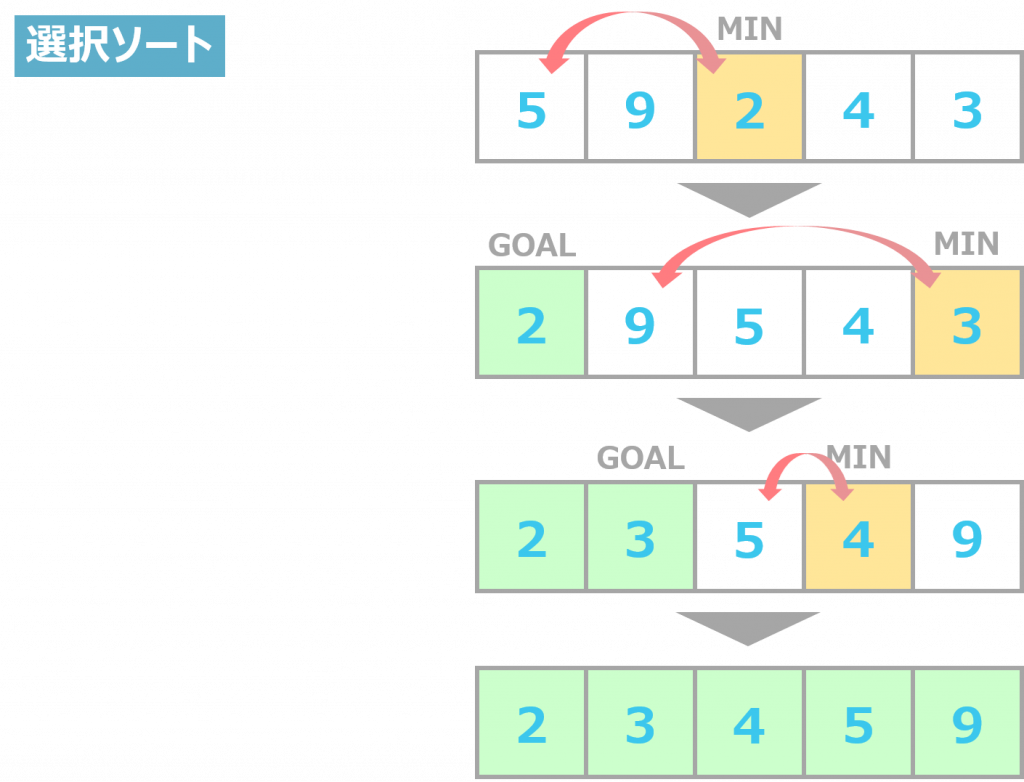
選択ソート

選択ソートは、データ群の中にある最小もしくは最大の数値を見つけ出して、データ群の1番左に移動させる方法です。

最も小さい（大きい）数字を見つけ出して移動させるだけなので、選択ソートの考え方は複雑ではありません。しかし、処理速度は遅く、安定性に劣ります。

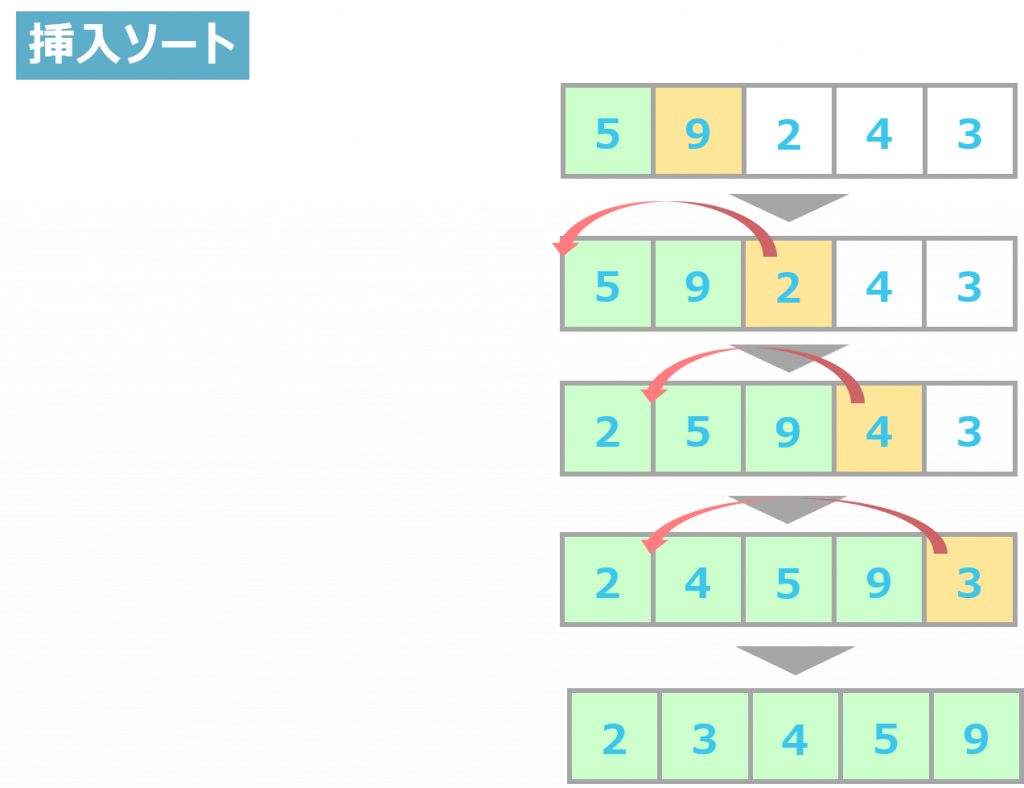
挿入ソート

挿入ソートは、整列済みの数値と整列済みでないデータ群の先頭の数値を比較して、ソートするアルゴリズムです。

ソートされていない要素を、整列済みデータの最後尾の数値と比較し、整列済みのデータの正しい位置に挿入します。整列されている部分が多いデータの場合、高速で降順に並べ替えることが可能です。

シェルソート

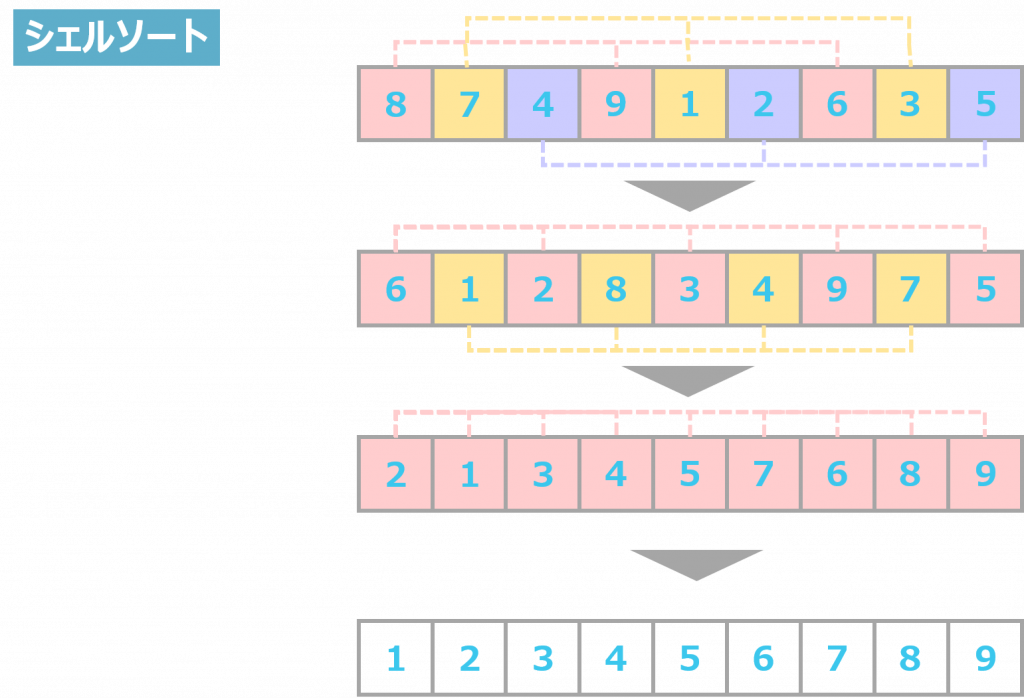
シェルソートは、一定間隔で要素を取り出し、取り出したグループごとに挿入ソートを行うアルゴリズムです。

先程、挿入ソートは整列済みのデータに強いことを述べました。シェルソートは、その性質を活かしたアルゴリズムになります。

クイックソート

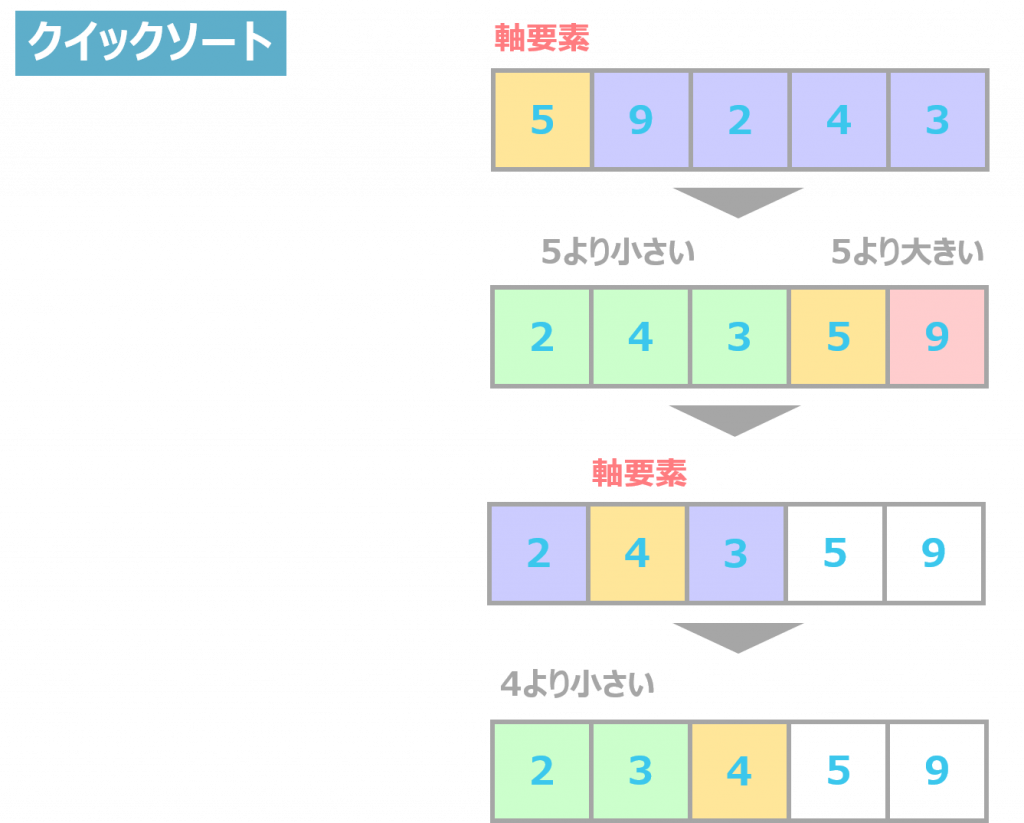
クイックソートは、データ群の中から特定の数値を軸要素として定めて、それよりも小さい数値を前に、逆に大きい数値を後ろに移動させるアルゴリズムです。

まずは、データ群の中からランダムに軸要素を決めます。その軸要素を基準としたソートが終了したら、軸要素よりも小さい数値と大きい数値、それぞれの中から再び軸要素を決めて、それぞれで数値を比較し、ソートを行います。この操作を繰り返すことで、最終的に数値を並べ替えることができます。

マージソート

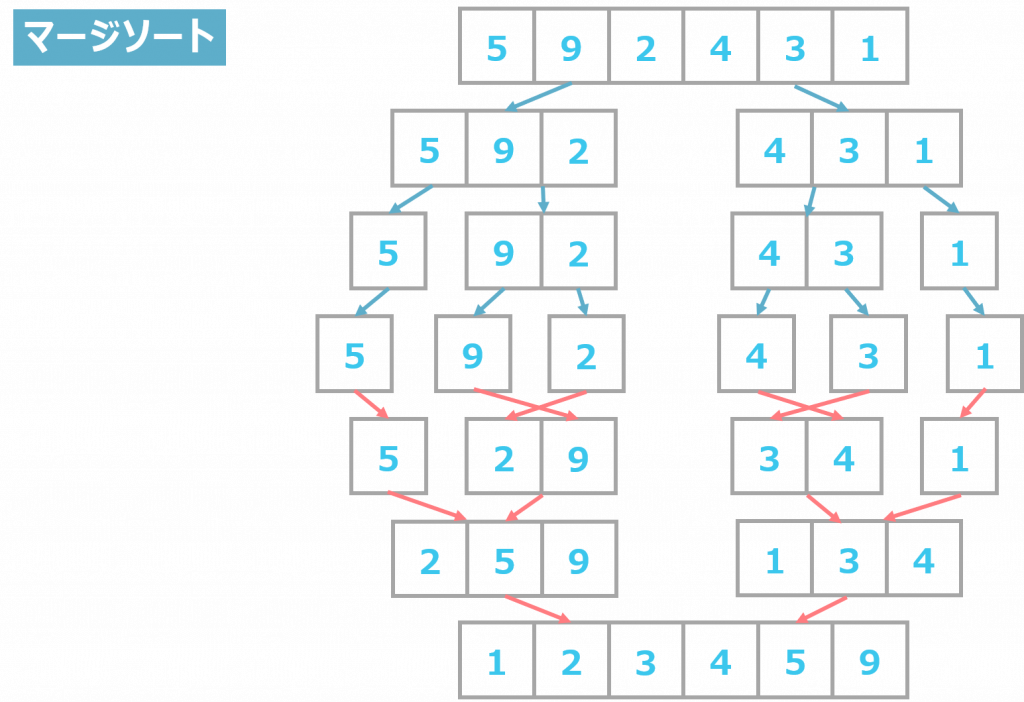
マージソートは、データを分割して整列させ、その後にマージさせて整列した数値のリストを作り上げるアルゴリズムです。

安定的なソートの実装が可能ですが、クイックソートに比べて計算速度は遅くなります。

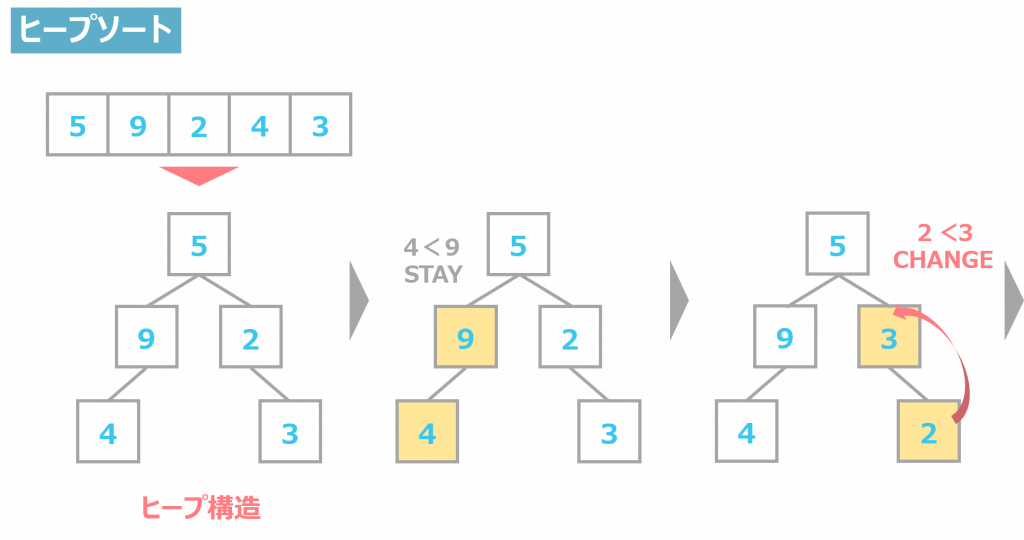
ヒープソート

ヒープソートは、ヒープ構造を構築しながらソートを行うアルゴリズムです。

ヒープ構造は、2分木のそれぞれの節目にデータを持っています。親データが2つの小データよりも小さくなるように作られており、木の根の部分がもっとも小さい数値であることが保証されるため、計算速度が速いという点がメリットです。

ヒープ構造については、この記事でのちほどご説明します。

再帰的アルゴリズム

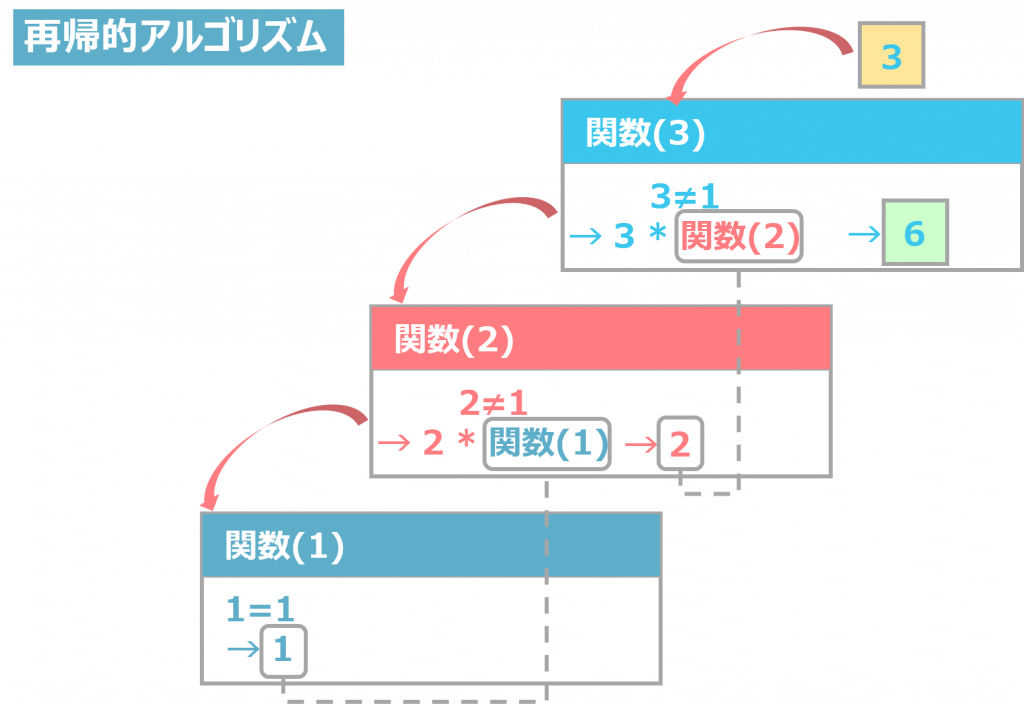
「再帰的アルゴリズム」とは、定義された関数の中で、返り値をその関数自身に設定して処理するアルゴリズムです。自身を呼び出す「再帰呼び出し」を用いて書かれたアルゴリズムである、と表現されることもあります。

関数が永遠に続くことを防ぐため、原則として再帰的アルゴリズムでは、関数を終了すべき数値を条件として設定します。そして、それ以外の数値では関数を呼び出すというようにコードを書くことが一般的です。

なお、再帰的アルゴリズムの例を以下に挙げています。

上記の例では、数値が1になったら再帰呼び出しを終了するという条件付けが行われています。数値が1以外の場合は、n-1の数値がudemy_factorial関数の引数に代入されて、再び呼び出されます。

　

データ構造の基本をわかりやすく解説

続いて、データ構造の基本とツリー構造について解説します。

基本のデータ構造

基本のデータ構造には、配列とリスト、スタック、キュー、ツリーがあります。

配列

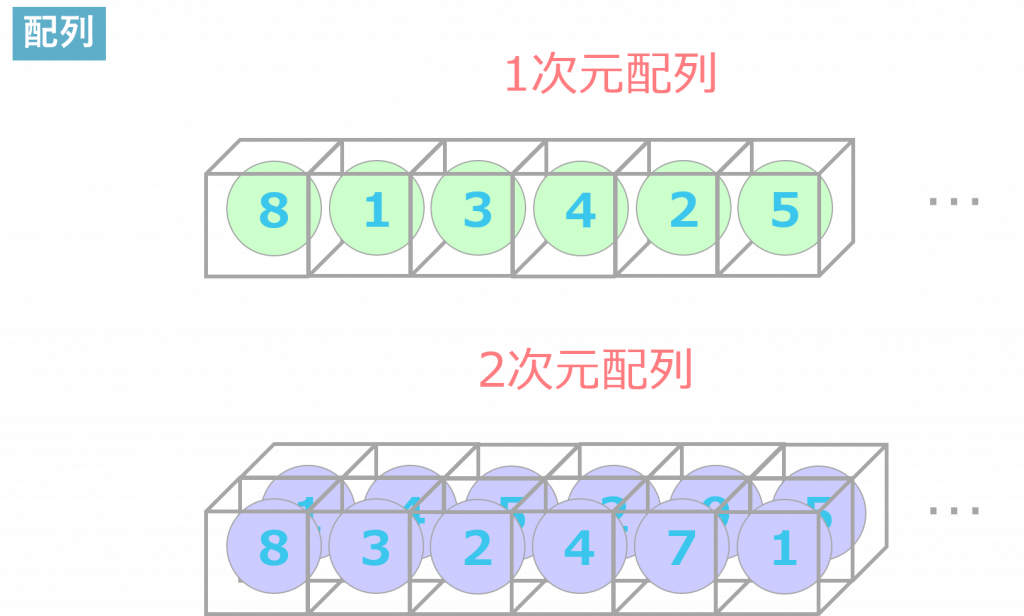
配列は大量のデータを保持するために使われるデータ構造です。配列には1次元配列と2次元配列があります。

1次元配列は、配列変数[添え字]という構造でデータを格納することが可能です。2次元配列は、配列変数[n1][n2]という構造です。n1は行番号、n2は列番号です。例えば、a[0][1]の場合、変数aの行番号0、列番号1の値を参照します。配列には3次元配列もあり、1次元配列以外を多次元配列と表現することも多いです。

リスト

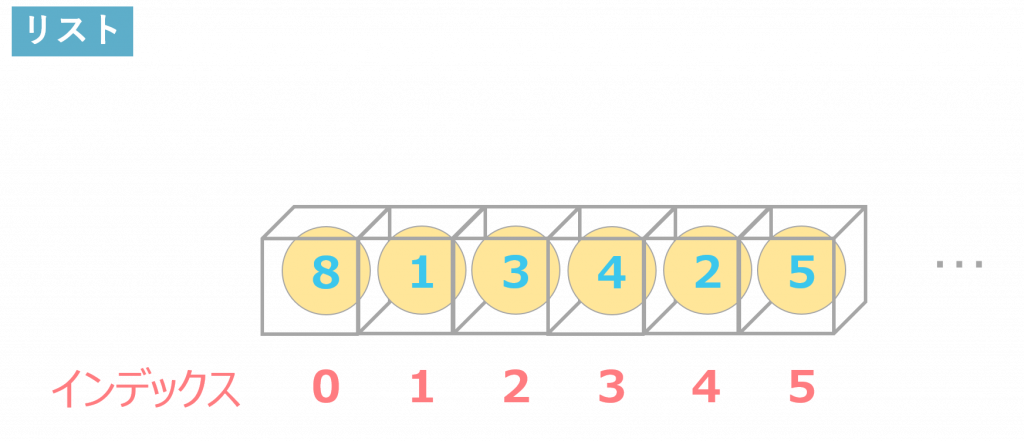
リストとは、それぞれの要素が順番に並んでいるデータ構造のことです。

それぞれの要素にはインデックス番号があり、要素へアクセスするときはインデックス番号を指定します。要素の数は自由に増やすことができ、格納する要素の型も指定がありません。

スタック

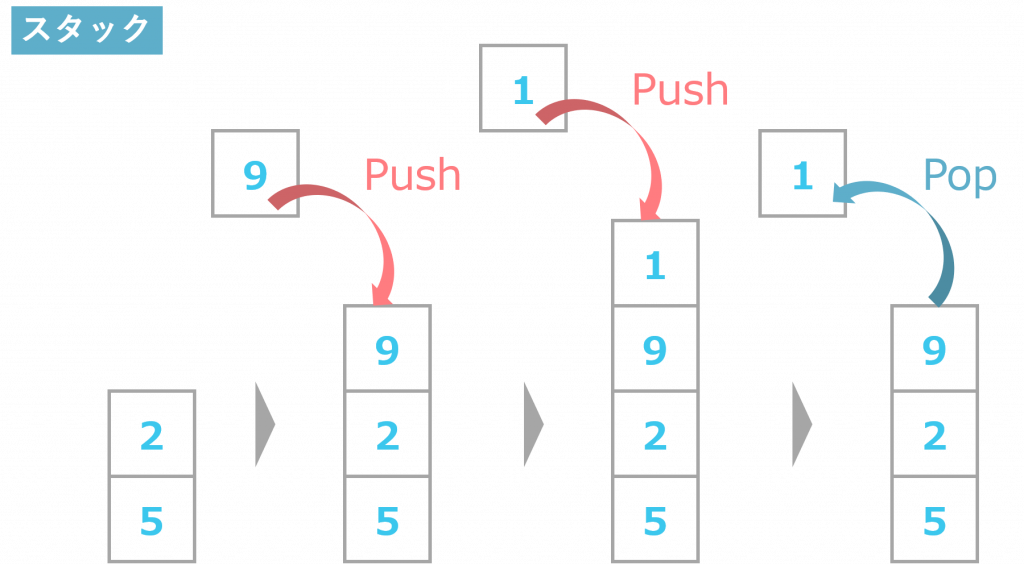
スタックとは、要素をブロックのように積み上げて格納できるデータ構造のことです。

箱を積み重ねていくように、挿入したデータは積まれたデータの1番上に格納されます。データを取り出す際も、1番上に積まれた要素から順番に取得され、1番上にあるデータ以外は取り出せません。スタックにおいては、データを積むことをプッシュ、データを取り出すことをポップと表現します。また、スタックにおける「最後に入れたものを最初に出す」データの出し入れのルールをLIFO（Last In, First Out）または「後入先出法」と呼びます。

キューとは何か

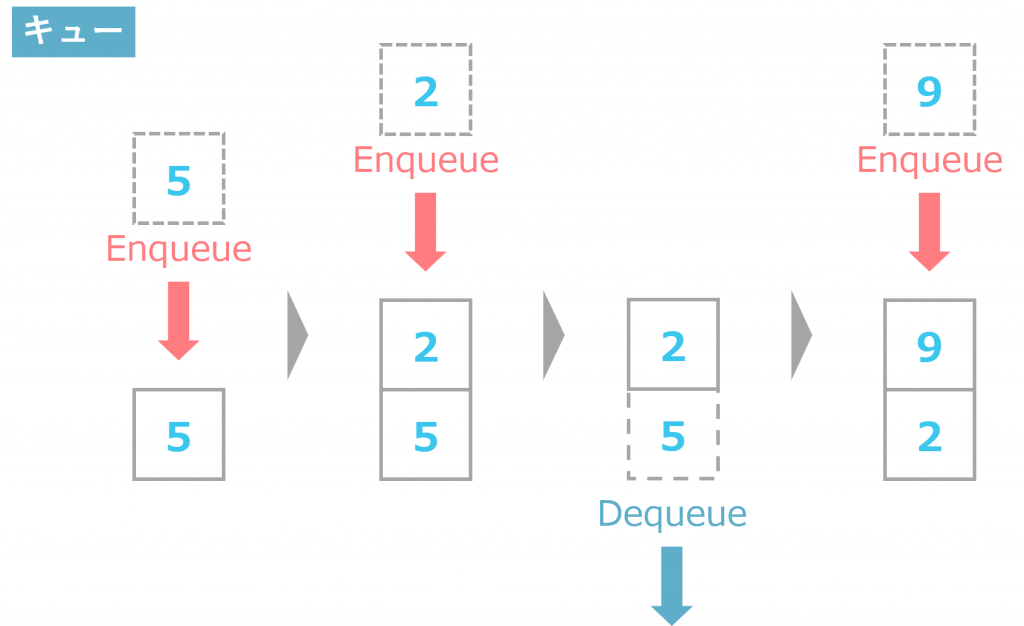
キューは、最初に格納したデータからしか取り出すことができないデータ構造のことです。

スタックでは、プッシュした最後の要素を最初に取り出しますが、キューにおいては、追加した最初の要素を最初に取得します。つまり、格納したのと同じ順でデータを取り出すということです。

キューにデータを追加することをエンキュー、データを読むことをデキューと表現します。また、キューにおけるデータの出し入れのルールをFIFO（First In, First Out）または先入先出法と呼びます。

ツリーとは何か

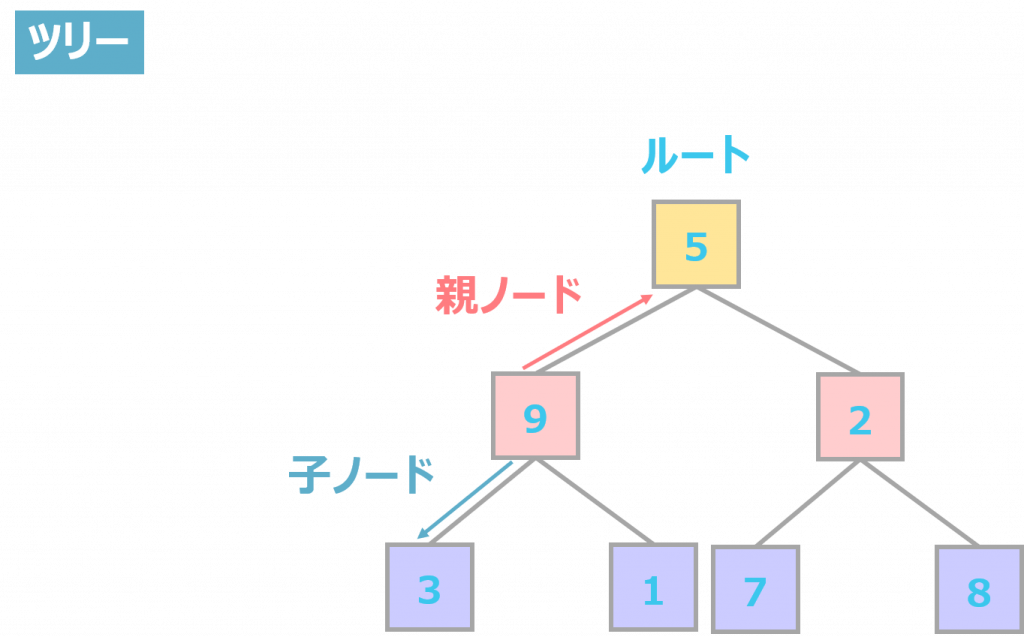
ツリーは、その名の通り木の形状をしたデータ構造です。階層構造と呼ばれることもあります。

木の根にあたる部分をルートと呼び、そこから親ノード、子ノードに派生していく構造です。

ツリー構造（木構造）

ツリー構造には、大まかにわけて3つの種類があります。

バイナリーツリー

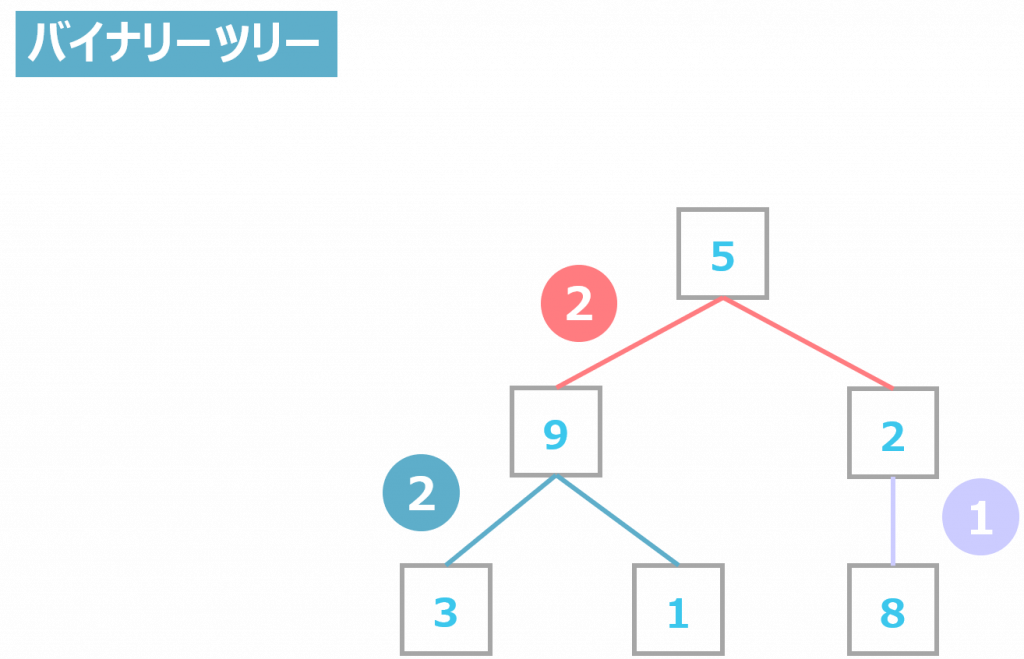
バイナリーツリーとは、ルート、親、2つの子までで構成されたツリー構造のことです。つまり、親は3つ以上の子を持ってはいけません。

バイナリーツリーは子が2つまでなので、構造がシンプルという特徴があります。

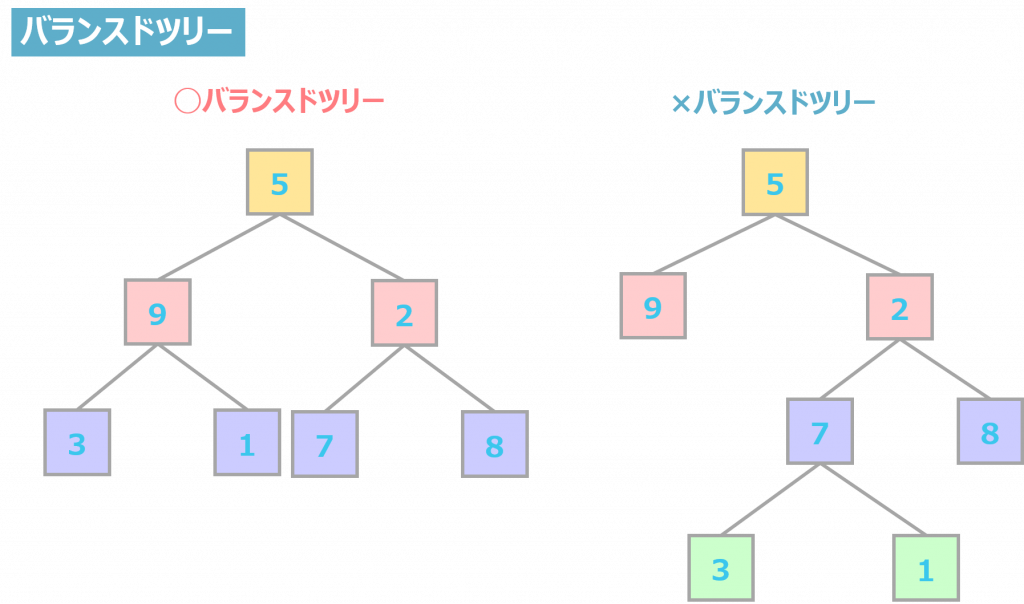
バランスドツリー

バランスドツリーとは、ルートノードから親ノードの距離を一定の長さにしたツリー構造のことです。

バランスを良くしてノードの数を減らすことを目的としており、これにより、処理速度の向上などが期待できます。

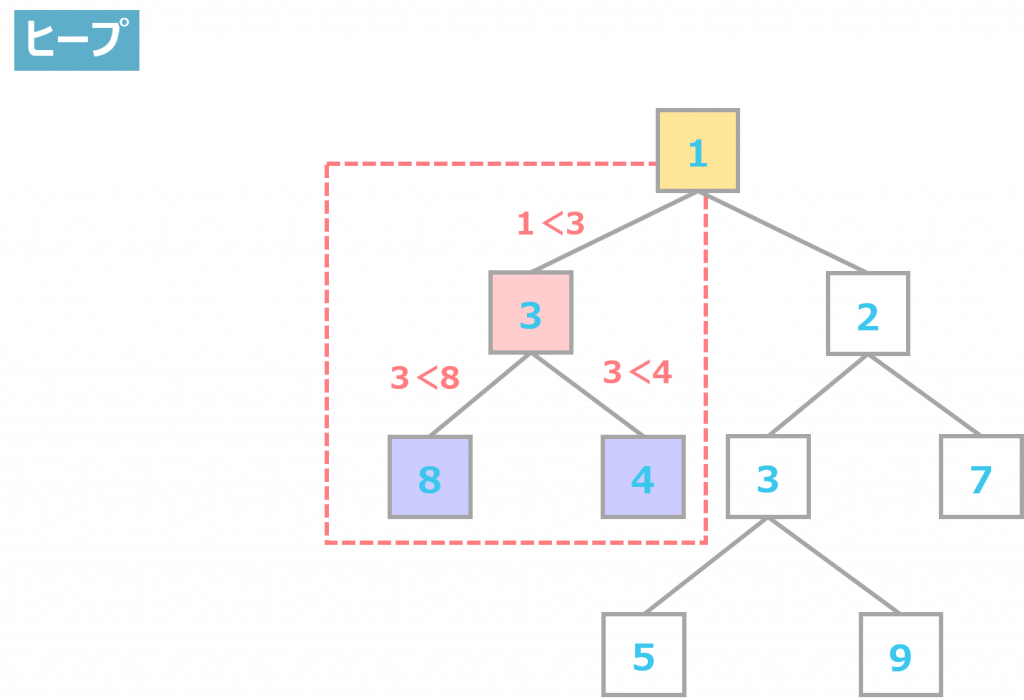
ヒープ

ヒープは、子ノードよりも親ノードのほうが小さいか、もしくは等しいという制限を設けて作られたツリー構造のことです。つまり、親ノードが子ノードの数を上回ることは禁止されています。

　

この記事では、アルゴリズムとデータ構造の基本を詳しく解説しました。アルゴリズムやデータ構造を理解しておくと、読みやすいコードを書けるようになったり、問題が発生した際にも柔軟に対応できたりします。アルゴリズムとデータ構造はエンジニアにとって必要不可欠の知識だといえます。ぜひ、この記事を学習の一歩としてお役立てください。