回帰分析(単回帰分析)をわかりやすく徹底解説！

近年はコンピュータの発達により、ビッグデータの活用に注目が集まっています。

データ分析に使うソフトウェアの性能も向上し、統計や分析の知識がなくてもデータ分析ができる時代になった、という声もあります。

しかし、コンピュータが出力する結果を適切に解釈し、ビジネスや実生活に応用していくためには、統計の知識がますます大事になってきています。

データ分析の方法はいろいろありますが、ここではわかりやすく実用的な「回帰分析」について、その中で最も単純で理解しやすい単回帰分析を取り上げ、丁寧に解説していきます。

公開日：2018年4月3日

回帰分析とは？…の前に、相関と因果の違いを解説！

まず、回帰分析の説明をする前に、データ分析に欠かせない「相関関係」と「因果関係」の違いについて説明しておきましょう。

相関関係

「２つの値の間に、一方の値が変化するともう一方の値も変化する」という関連性があれば、相関関係があるといいます。

この時、２つの変数の間に、原因→結果の関係は必要ありません。

つまり、疑似相関の関係（実際には剰余変数が存在する場合や、全くの偶然）である可能性もあります。

例えば「猫が顔を洗うと雨が降る」ということわざがありますが、これは「（原因）猫が顔を洗う（頭部のグルーミングをする）→（結果）雨が降る」のではありません。

「（原因）雨が降る前兆（低気圧の接近や湿度の上昇）が現れる→（結果）前兆にストレスを感じた猫が、ストレス発散やヒゲの感度を保つために顔を洗う→実際に雨が降る」という流れです。

なお、相関の強さは相関係数で表すことができます。

相関係数は通常rであらわされ、-1≦r≦1の範囲をとります。

0は相関がないことを表し、0より-1、1に近い値であるほど強い相関があることを表します。

因果関係

”原因→結果”の方向性を持った関係を因果関係といいます。

「因果関係がある」というためには、２つの変数の間に”原因→結果”の方向性がある「原因と結果の関係」が存在する必要があります。

データ分析の際に役立つのは、この因果関係の方です。

相関関係と因果関係は、混同して使われることがよくあります。

しかし、内容は全く異なるものです。

このため、回帰分析の結果は因果関係の証明にはなりません。

これは、回帰分析を行う上で押さえておくべき重要なことです。

回帰分析とは？そもそもどんなもの？

回帰分析とは、関数をデータに当てはめることによって、ある変数yの変動を別の変数xの変動により説明・予測・影響関係を検討するための手法です。

説明したい変数yを目的変数、それを予測するための変数xを説明変数とよびます。

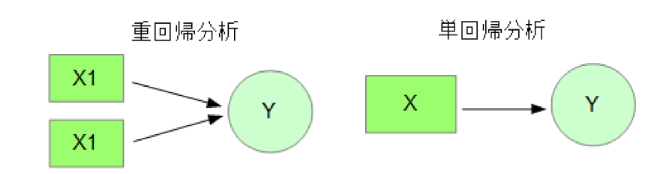
ここで説明する単回帰分析は、説明変数が１つの回帰モデルです。

説明変数が１つなので、y=ax+bのグラフの形、つまり線形の関係を仮定して目的変数を予測します。

グラフの形から、線形単回帰分析ともよばれます。

単回帰分析だけでは因果関係の特定はできませんが、その推論の手がかりにはなります。

説明変数が二変数以上になる回帰分析を「重回帰分析」といい、より高度な分析が可能となります。

なお、「回帰」という言葉は、英国の遺伝学者であり統計学者でもあったゴールトンの「平均への回帰」という概念が語源となっています。

興味がある方は、ぜひ調べてみてください！

回帰分析のやり方を紹介！

実際の回帰分析の手順は、次のようになります。

①(架空or各種統計資料などの)２変数のデータをプロットした散布図を作成

②一次関数でy=a+bxなどの回帰式を仮定し、最小二乗法によりa,bの値を決定

③(煩雑になるので最小二乗法を実際にやらずに公式に当てはめて)回帰式を決定

④回帰式をグラフに書き入れ、そこから情報を読み取る(横軸が１単位ずれると縦軸ではどれだけズレるかなど)

実務では、④の後、残差(予測値と実際の値のズレ)について分析したり、決定係数の算出などにより信頼性・妥当性の検証もしていきます。

単回帰分析だけでできることはさほど多くありません。しかし、発展させて重回帰分析につなげていくことで、深い分析が可能となります。
基礎的なツールとしてまずは単回帰分析をしっかり理解し、使いこなせるようにしましょう。

回帰分析のメリット・デメリットは？

回帰分析のメリットとデメリットについて、簡単にまとめてみました。

分析手法に迷っている場合には、是非参考にしてみてください。

メリット

・散布図に直線を当てはめることで関係を見ようとするというわかりやすさ
・数字を使って予測することで統計的な、根拠ある推論が可能になる
・データがないところについても予測が可能となる

デメリット

・剰余変数の存在などがあることに気づかないと誤った推論になりかねない(判断するのはあくまでも人間)
・実際の分析では重回帰分析を用いることが多く、単回帰分析が活用できる場面は限られる

もっとも、回帰分析の本質を理解し、適切な使い方をすれば、ここで挙げたデメリットもデメリットではなくなるでしょう。

回帰分析を活かそう！回帰分析の活用法

最後に、ビジネスやマーケティングなど、回帰分析の実生活における応用例を紹介していきます。

例１：家賃の予測
単回帰分析：目的変数「家賃の高さ」を、説明変数「広さ」だけで推論する。
重回帰分析：目的変数「家賃の高さ」を、複数の説明変数「広さ」「築年数」「駅からの近さ」などの様々な要素で推論する。

例２：広告クリエイティブの最適化予測
単回帰分析：目的変数「広告のクリック率」を、説明変数「背景」だけで推論する。
重回帰分析：目的変数「広告のクリック率」を、複数の説明変数「背景（色,模様、質感など）」「フォーマット」「素材（各種）」「企業自身の分析力」などの様々な要素で推論する。

データ分析は、エクセルなどのツールを使うことで簡単にできます。
しかし、適切な推論をする上で、その背景を知ることはとても重要です。

実際に数式を使って理解するには、動画等の教材を使うのがベストです。
これを機に、動画講座で統計について理解を深めてみてはいかがでしょうか？

評価：★★★★★
非常に分かりやすい講義内容でした！
業務でも統計視点でみる機会が増えてきたので、基礎から学び直ししたく受講しました。これまで単に関数処理していた数値の根拠を知ることができ、感謝します。

評価：★★★★★
シグマ先生の授業は超絶分かりやすくて、勉強になります。統計検定の勉強のため大変参考になります。難しい内容も平易に説明をしてくださったり、図も提示してくださること、また語り口も理解が進む雰囲気であると感じました。