近年、よく耳にするようになった「ビッグデータ」「機械学習」「データサイエンス」といったテクノロジー。これらに共通しているのは、「膨大なデータが出力される」という点です。
そして、そのデータの統計をとるうえでは、「標準偏差」「分散」のような値が欠かせません。
こちらでは、データのばらつきが可視化できる標準偏差の定義や、エクセルでの求め方、グラフの作成方法などについてご紹介します。
\文字より動画で学びたいあなたへ/
Udemyで講座を探す >INDEX
標準偏差とは何か? 分散との違いもわかる
標準偏差とは、統計学の分野において複数データ間のばらつきの大きさを示す値です。一般的にσ(シグマ)、もしくは5で表され、算出には以下の公式を用います。
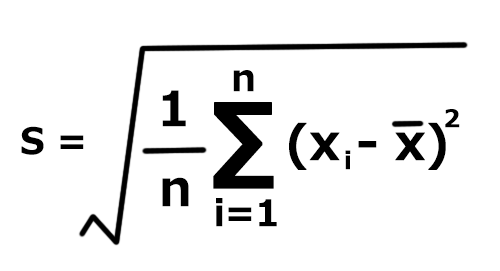
各データの数値からデータ全体の平均を差し引いた値の二乗を合計し、さらにデータの総数で割った値の正の平方根が標準偏差です。
標準偏差と同じようにデータのばらつきを示す「分散」という値が存在します。基本的な公式の成り立ちはまったく同じですが、標準偏差が最終的に正の平方根を求めるのに対し、分散の算出では平方根を求めません。つまり、分散は標準偏差を二乗した値ということになります。
標準偏差は最終的な単位がデータと同次元ですが、分散は単位についても二乗となります。そのため、現実に存在するデータのばらつきを測定する際は、データと同次元でイメージがしやすい標準偏差が用いられる傾向があるようです。
\文字より動画で学びたいあなたへ/
Udemyで講座を探す >標準偏差を使えば何がわかるの? 具体例で解説
標準偏差でわかるのは、複数データ間における特定データの希少性や優劣です。今回は2つの例を紹介します。
【ケース①】テストの点数の標準偏差
例として、複数人のテストの点数を比較するケースを想定してみます。
| 名前 | テストの点数 |
|
A |
32点 |
|
B |
85点 |
|
C |
74点 |
|
D |
53点 |
|
E |
66点 |
|
平均点 |
62点 |
A~Eの5人のテストの平均は62点となっています。平均点を超えているのは、B、C、Eの3人です。
この時、標準偏差を求めると、
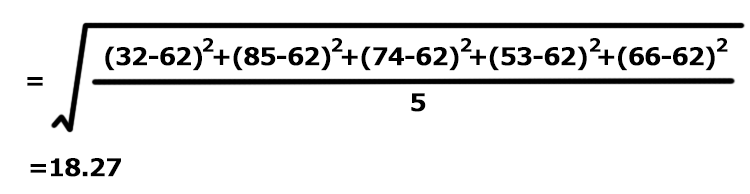
となりますから、比較的データのばらつきは大きいと判断できます。
つまり、Cは平均点を超えているが、それほどすごくないと考えられます。
逆にDのように53点でも、あまり気にしなくても良いと判断できます。
標準偏差が小さい場合には、ばらつきが少ないため、平均点を上回っている人は、すごいと判断できます。
【ケース②】複数支店の売上比較
続いて例として、複数支店の売り上げを比較するケースを想定してみます。
| 支店名 | 売上金額 |
| A | ¥3,000,000 |
| B | ¥4,500,000 |
| C | ¥2,000,000 |
| D | ¥800,000 |
| E | ¥1,000,000 |
| F | ¥6,000,000 |
| 売上合計 | ¥17,300,000 |
| 売り上げ平均 | ¥2,883,333 |
この表を見る限り、支店Aの売り上げは各支店の平均値を突破しており、優秀に見えます。しかし、単純に統計データの総和をサンプル数で割った平均値から特定データの優劣を判断する考え方は、必ずしも正しくありません。
一部支店が、高い売り上げを出していたとしても、多くの支店の低い売り上げによって平均が下げられているケースが考えられます。このようなケースでは、平均よりも売り上げている店舗を称賛するよりも、売り上げの低い店舗を問題視しなければなりません。
店舗Aの売り上げが本当に優秀な数字かどうかは、標準偏差からわかります。標準偏差の値が小さければ、店舗Aは激しい競争のなかで平均以上の売り上げをたたき出した優秀な店舗ということです。対して標準偏差の値が大きければ、一部の店舗が平均を下げているだけで、店舗A以上の売り上げを出している店舗はたくさんあるということになります。
例としてあげた表の場合、標準偏差は約1,871,120円(桁が大きいため、以降の章で求め方は説明します)。全体的にばらつきが大きく、平均を越えているからといって店舗Aの売り上げを手放しで評価できないことがわかります。
標準偏差をエクセルで求める方法(STDEV.P関数)
標準偏差を、手計算で算出するのは時間がかかります。一方、エクセルを用いれば、もととなるデータさえあれば簡単なやり方で算出可能です。「STDEV関数」を使った、標準偏差の算出方法をご説明しましょう。
1.もととなるデータを入力し、標準偏差を入力したいセルを選択します。
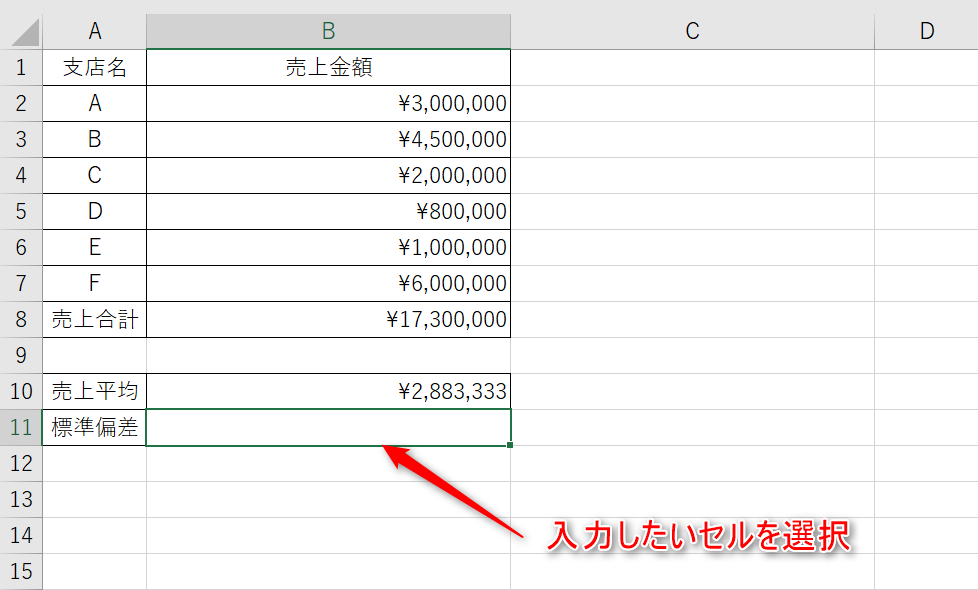
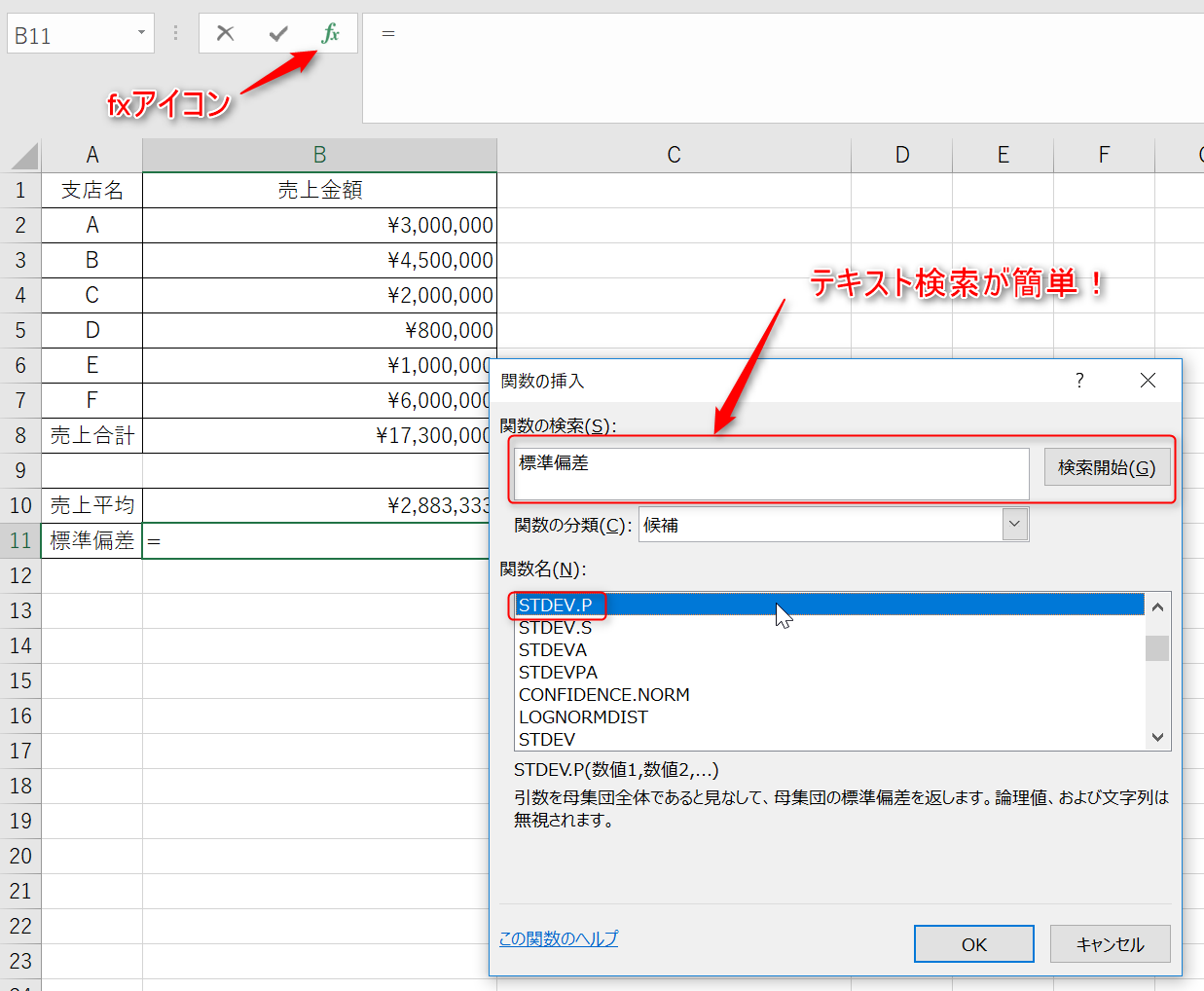
2.目的のセルが選択されたままの状態で上部のfxアイコンをクリックし、P関数を見つけましょう。「標準偏差」と検索すると簡単です。STDEV.P関数を選択したら、「OK」をクリックしてください。
3.関数の引数として、各データを指定しましょう。表のデータをドラッグするだけです。
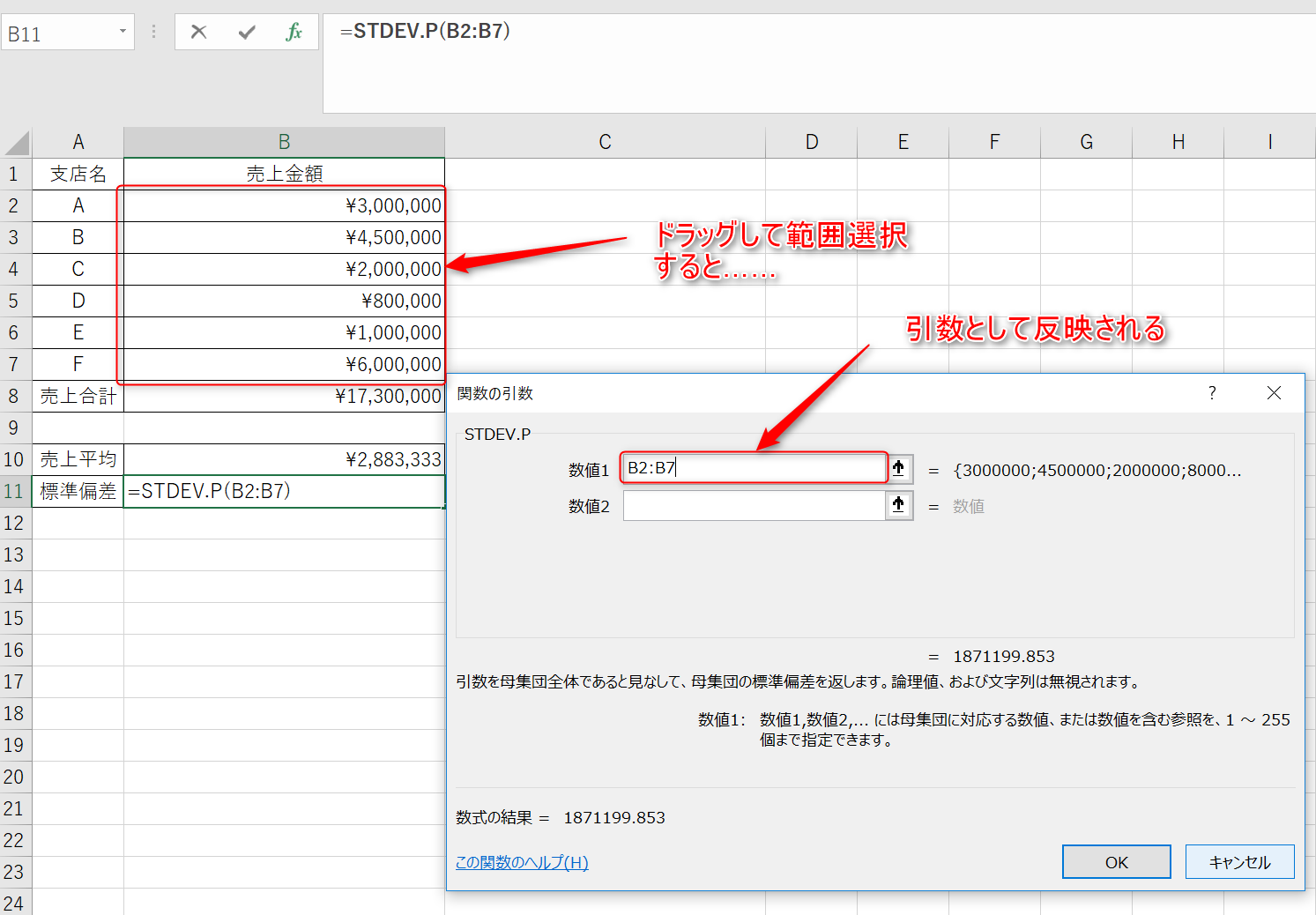
4.最後に「OK」をクリックすれば、指定していたセルに標準偏差の値が入力されます。
エクセルで標準偏差を求める時に必要なSTDEV.PとSTDEV.Sの違いとは?
STDEV関数には、上述した方法で紹介したSTDEV.Pのほか、「STDEV.S」が存在します。どちらも平均値からのばらつきを求める関数として定義されていますが、使い分けが必要です。引数として指定されたデータのばらつきを求めるSTDEV.Pに対しSTDEV.Sはデータの抽出もとの母集団におけるばらつきの推定値が算出できます。
多数の店舗のなかから無作為に選びだした対象のみについて売り上げのばらつきを求めたい場合は、STDEV.Pを用います。対して、店舗全体における売り上げのばらつきを推定したい場合に用いるのがSTDEV.Sです。
エクセルで求めた標準偏差を適切なグラフで表現する方法
エクセルで求めた標準偏差、および平均値は、グラフを作成する要素として用いられることもあります。標準偏差を用いたグラフのなかでも、代表的な棒グラフ、正規分布曲線をエクセルで作成する方法をご紹介しましょう。
棒グラフ
データの平均に対する標準偏差は、棒グラフにおける誤差範囲として表示できます。具体的な手順をマスターしましょう。
1.平均値、標準偏差が算出された表を用意します。
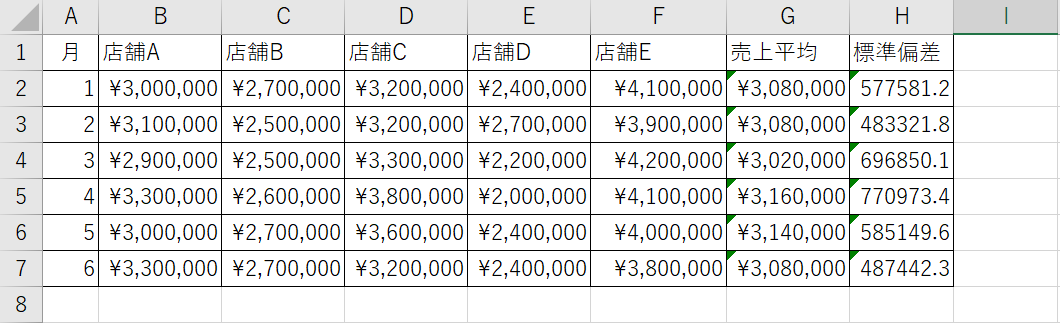
2.平均値の棒グラフを作成しましょう。対象となる平均値をすべて範囲選択し、「挿入」タブにある「おすすめグラフ」をクリックします。
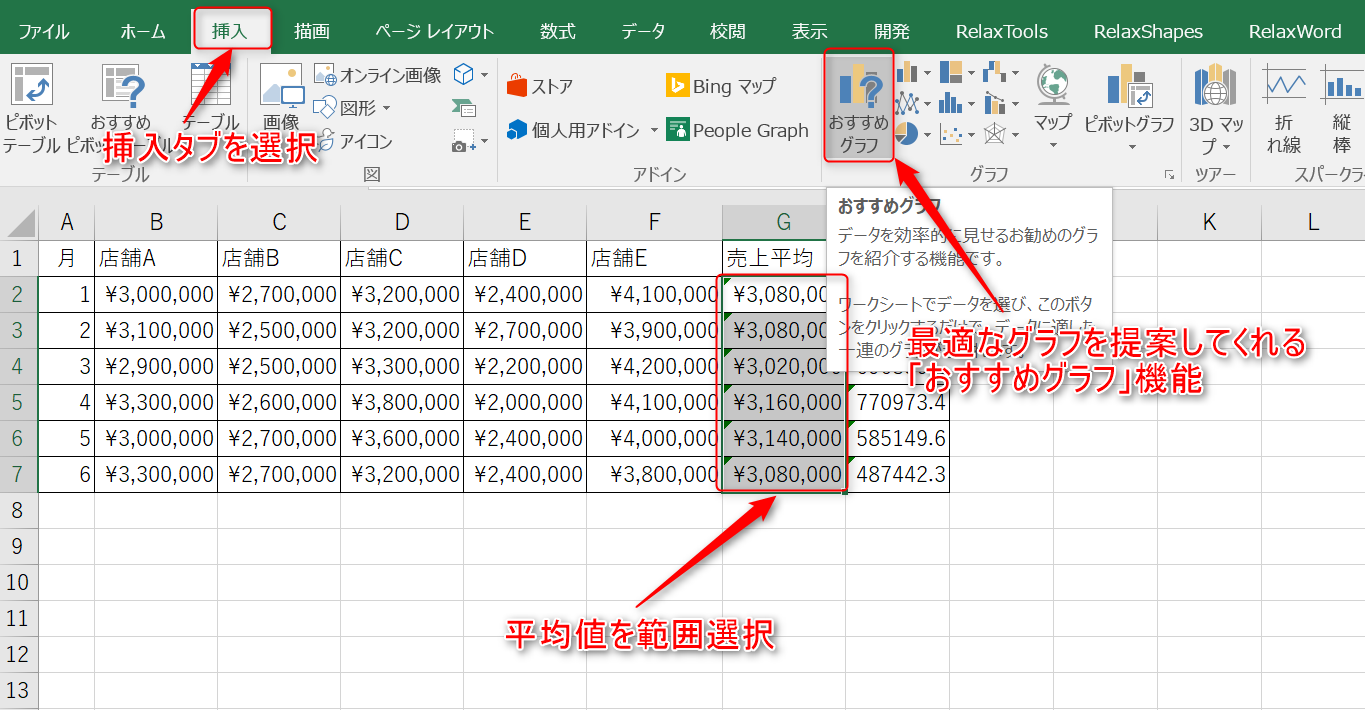
グラフの挿入ウィンドウの中から、「集合縦棒」を選択してください。
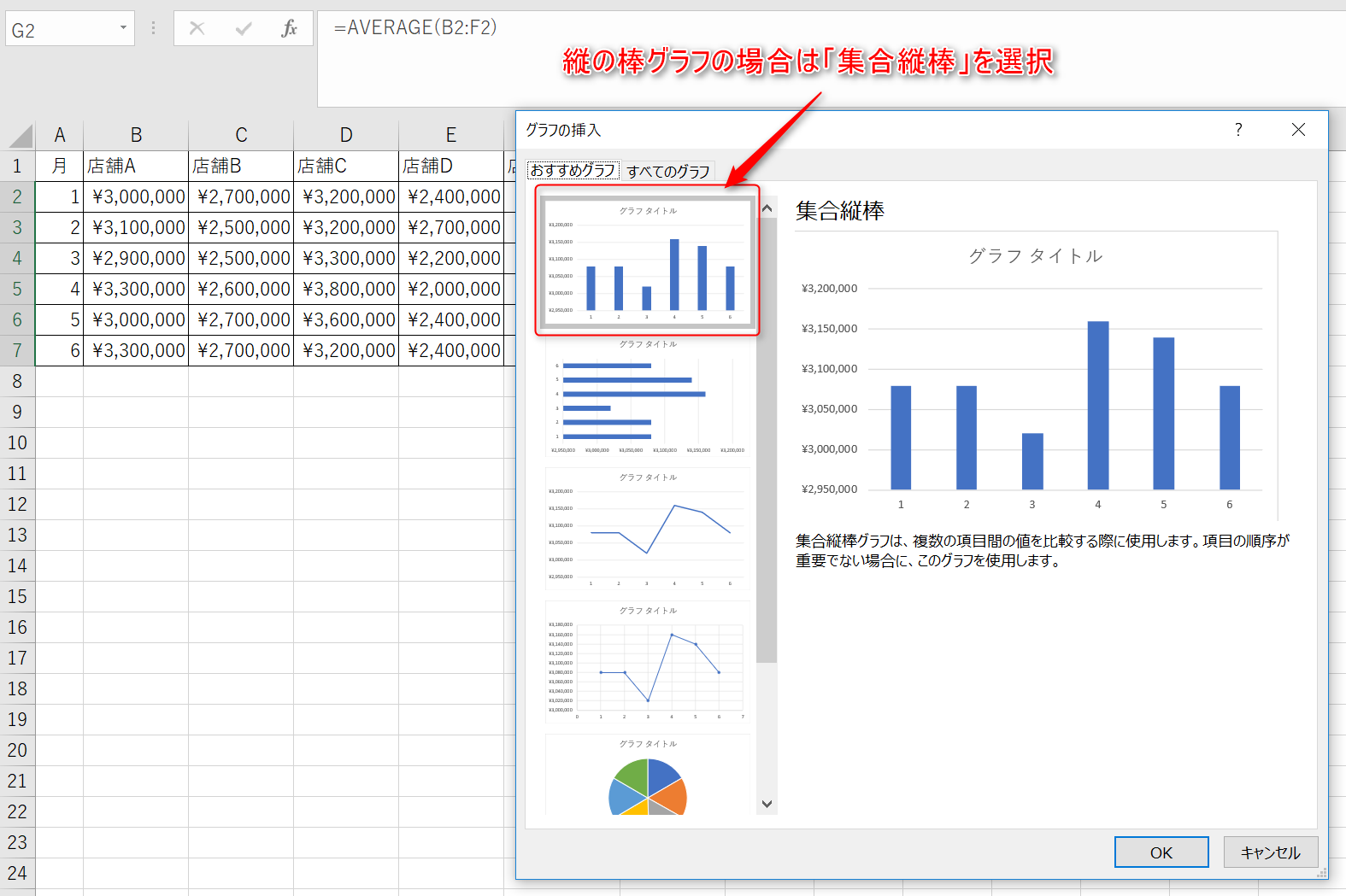
3.平均値のグラフに、標準偏差の情報を誤差範囲として付加します。
グラフを選択し、「グラフツール」のデザインから「グラフ要素を追加」をクリックしてください。クリックすると現れる「誤差範囲」から、「その他の誤差範囲オプション」を選択してください。
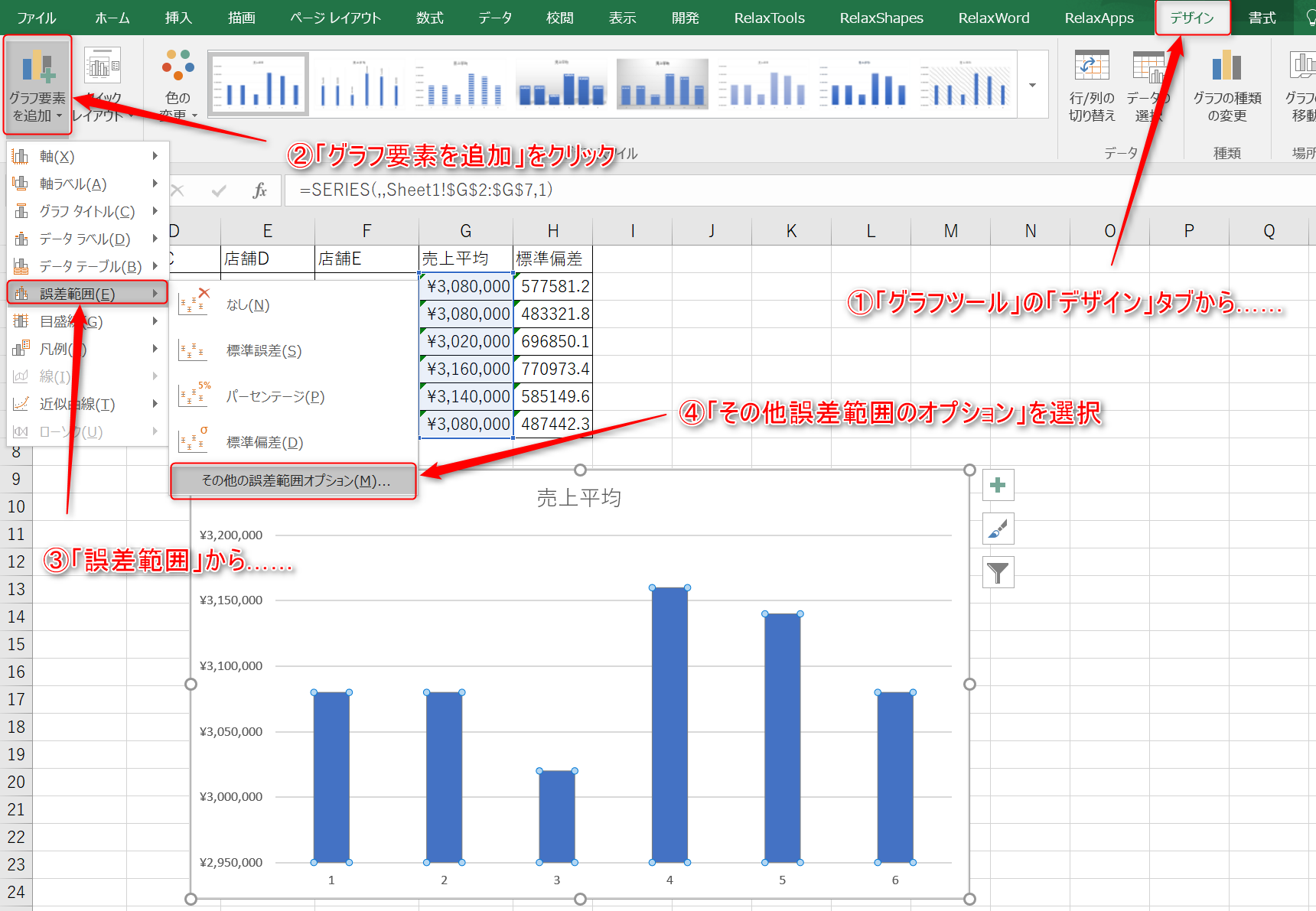
4.ばらつき情報に算出された標準偏差を反映するためには、誤差の値をユーザー側で指定する必要があります。
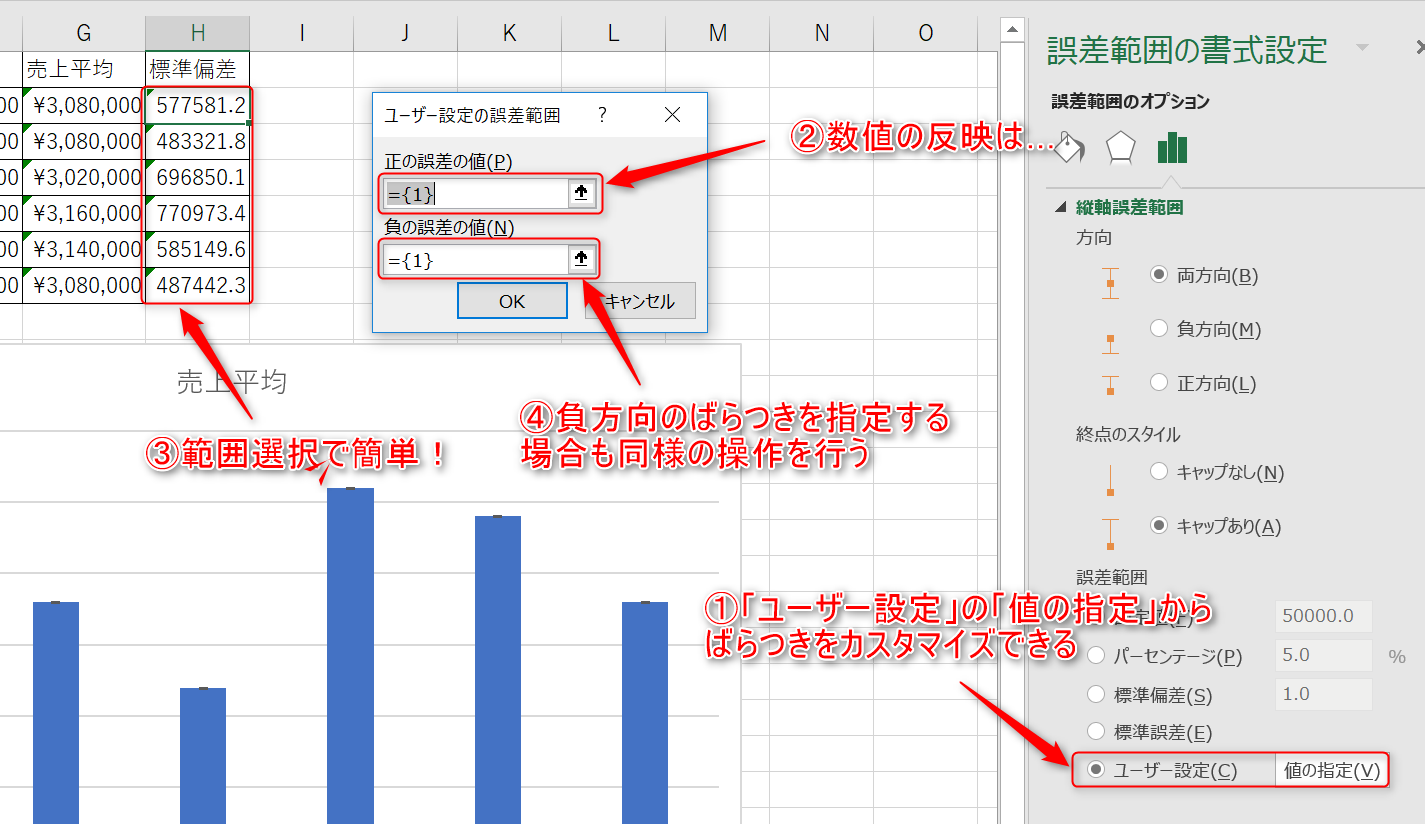
「誤差範囲の書式設定」下部の「誤差範囲」から「ユーザー設定」を選択後に「値の指定」をクリックし、標準偏差を正の誤差として指定しましょう。
負方向のばらつきも表示させたい場合は、負の誤差にも同様に標準偏差を指定します。
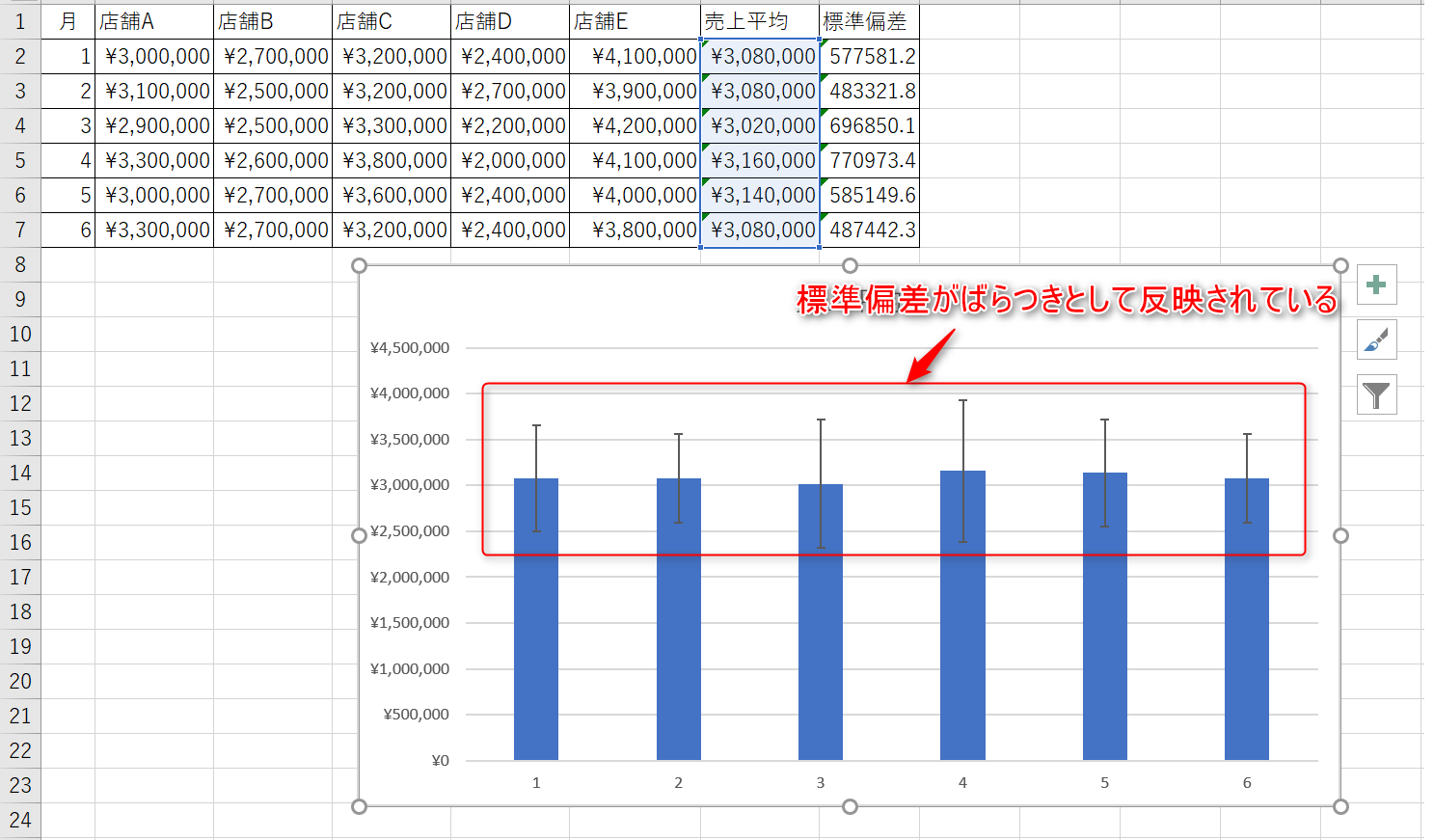
5.平均の棒グラフに各平均に応じた標準偏差が表示されたら完成です。
正規分布曲線
平均値と標準偏差の値があれば、その平均値を中心とした正規分布曲線を描くことができます。
1.正規分布曲線を描くための表を用意します。x軸の広さは、平均±3s程度が目安です。
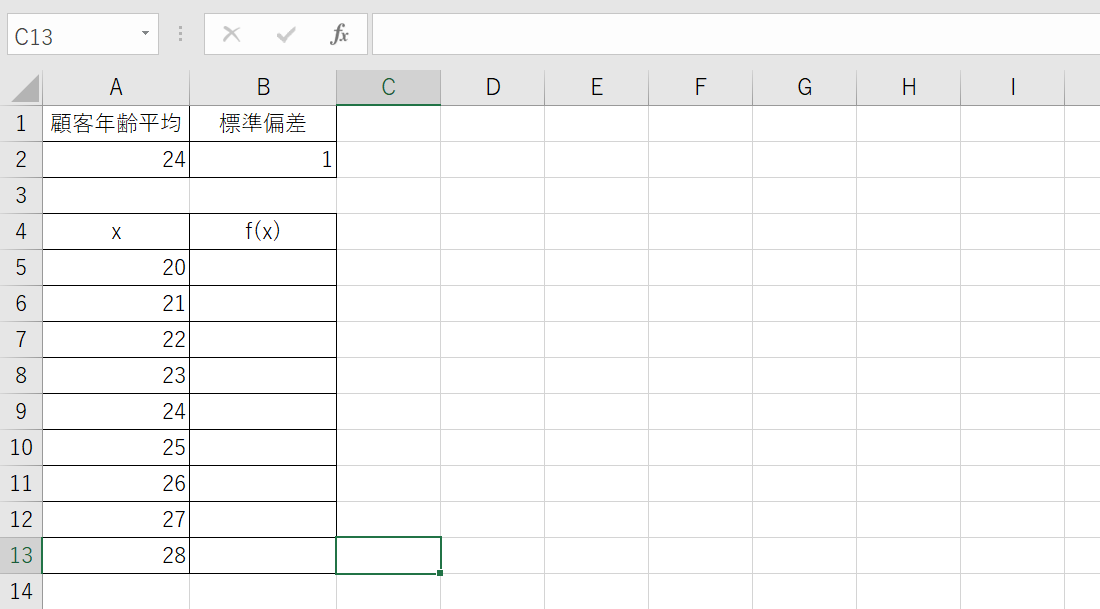
2.エクセルには正規分布を求めるための「DIST関数」が用意されています。xには対応するx軸の値を、平均、標準偏差にはあらかじめ算出した数値を引数として入力してください。関数はFALSEを用います。
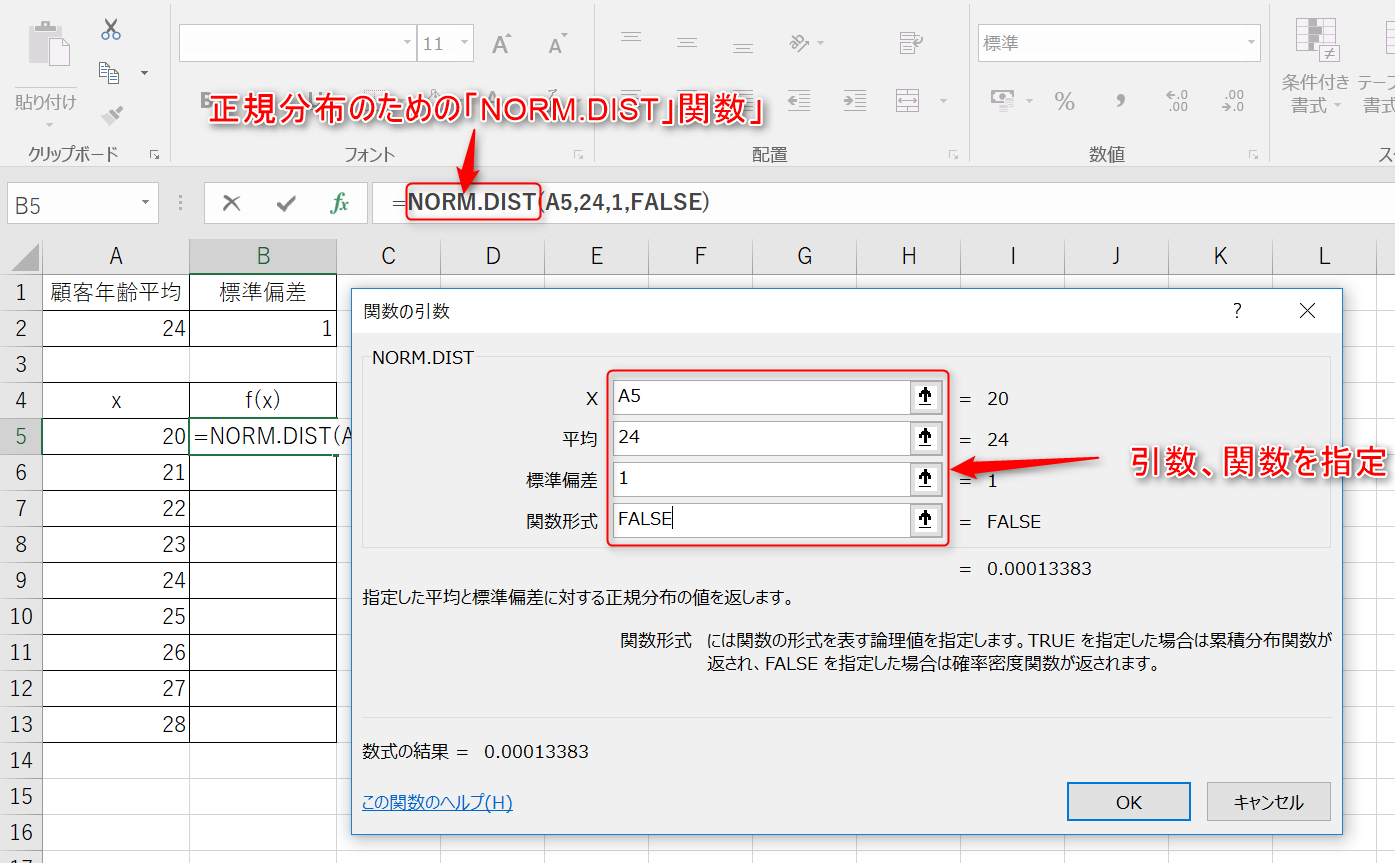
3.それぞれのセルに同様の関数を入力し、xに対応したf(x)の値を算出しましょう。
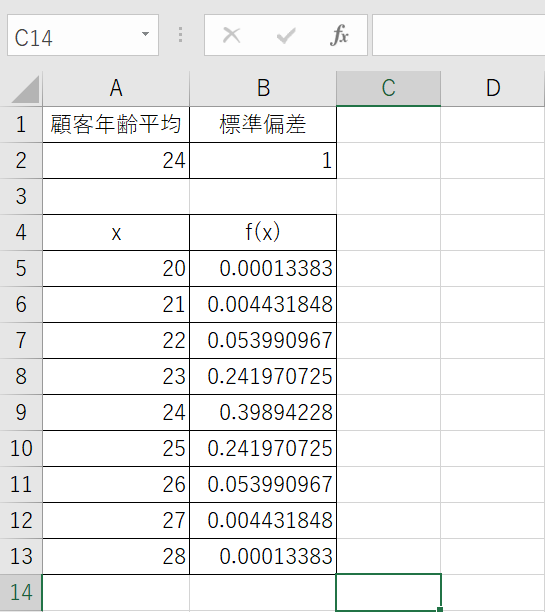
4.すべてのxとf(x)を範囲選択し、「挿入」タブから作成するグラフを選択します。正規分布曲線を描く場合、「散布図(平滑線)」を使うのが一般的です。
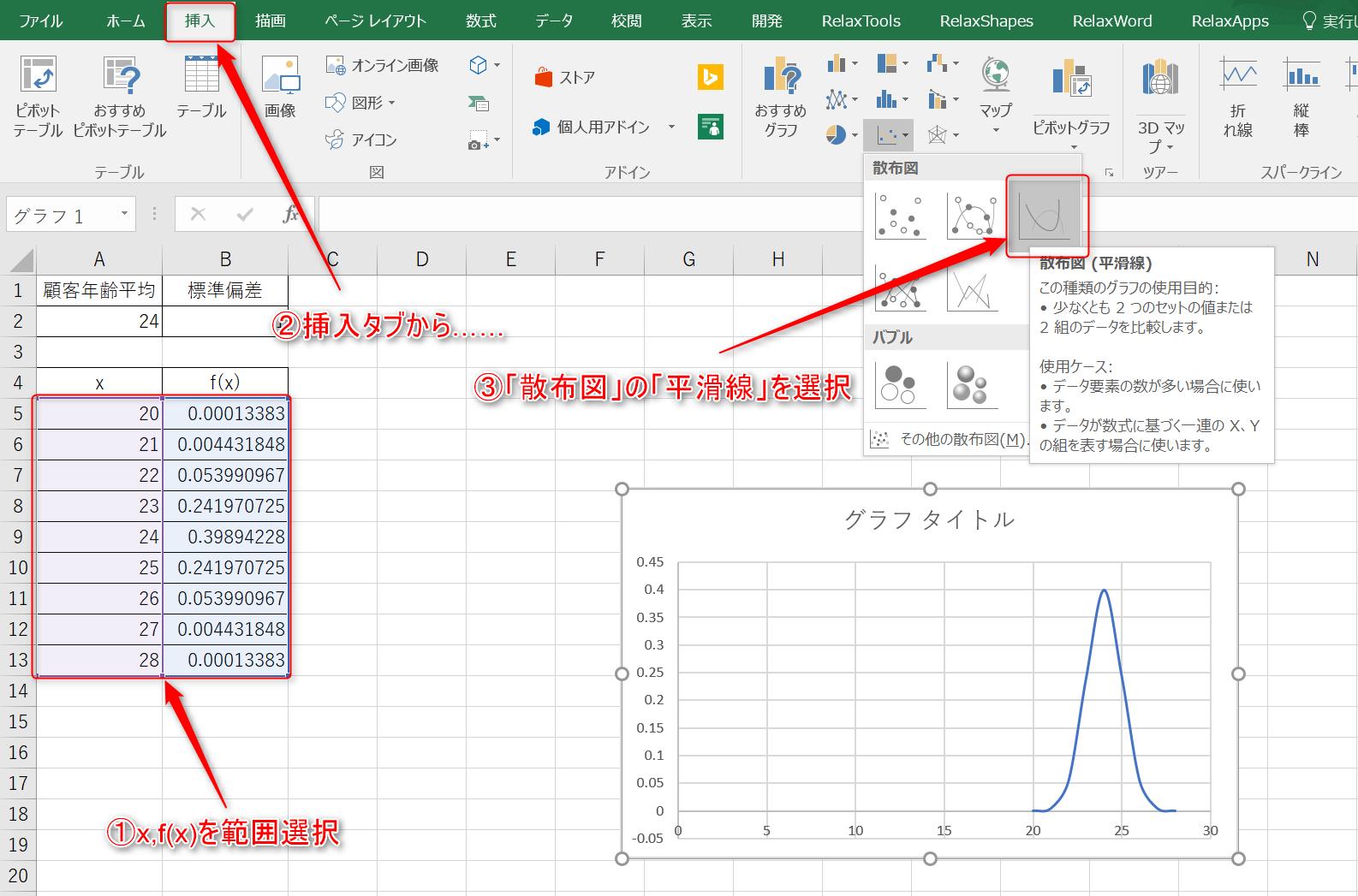
いかなる産業、業種においても、測定されるデータは常にばらつきます。
標準偏差、分散は、そうしたデータの統計をとるうえで、捨て置くことのできない、基本的な考え方です。標準偏差から読み取れることをしっかりと把握し、通常業務のなかで活かせるポイントを見つけてみましょう。
いかがでしたでしょうか?
Udemyでは、初心者の方向けにエクセルに関する講座を多数用意しています!
また、MOS試験対応の講座も用意しています。
これを機に、ぜひエクセルを使えるようになりましょう!














最新情報・キャンペーン情報発信中