ベイズ統計は通常の統計とは異なり、得られたデータの方を重要視し、そこから何が言えるのかを推定します。
結果は、「得られたデータから~~ということが~~%言える。」といった形で表すことができます。
データが全くない場合は1/2となる確率を、データを得るたびに修正していきます。つまり学習能力があるということです。
今回紹介するツール「stan」では、ベイズ推定を高速でかつ効率よく行うことができます。
\文字より動画で学びたいあなたへ/
Udemyで講座を探す >ベイズ統計を高速で処理できるstanとは?ベイズ統計もおさらい!
stanとは統計モデリングやデータ分析、予測に使える統計的計算のための最先端のプラットフォームです。
stanはベイズ推定を高速で行うことができるのが特徴です。
ベイズ統計では、確率についての考え方が重要です。
まず確率には「客観確率」と「主観確率」の2つがあります。
前者は「サイコロを1回振って1が出る確率が1/6」といったものです。
後者は「家から駅に向かうまでに女性とすれ違う確率」という、住んでいる家の場所など、個人の主観によっても変化する確率のことを指します。
ベイズ統計は2つのうち、主観確率を扱う統計です。
また、主観確率には「事前確率(事前分布)」と「事後確率(事後分布)」の2つがあります。
実はベイズ統計の考え方は無意識のうちに私たちが行っていることでもあります。
例えば以下の会話をイメージしてみてください。
取引先の部長「うちの子も中学生になってね。子供1人でも結構お金がかかるよ。」(お子さんは1人ということか)→男50%女50%
部長「この前もピアノを習いに行きたいと突然言い出して。」(ピアノ?女の子かな?)→男30%女70%
部長「親としてはもう少し外で遊んでほしいのだけれど。。」(実は男の子なのか?)→男40%女60%
部長「でも、男の子だと一緒に遊びやすいね。」(男の子だったか)→男100%
このように、最初は半々だった男女の確率ですが、話が展開していくに連れて変化していきます。
ベイズ統計では、こういったことを計算式で求めるのです。
ベイズ統計について、詳しくはこちらの記事をご覧ください。
\文字より動画で学びたいあなたへ/
Udemyで講座を探す >どうしてstanが必要なの?
では、どうしてstanが必要なのでしょうか?ここでは、stanを使用することの利点をご紹介します。
ベイズ推定では、得られたデータを学習データとしてどんどん追加していくことで精度を上げていくので、一度実行したデータに効率良く新しいデータを入れていく必要があります。
従来のツールではデータが変更や追加されるたびにデータのセット、イニシャライズ(初期化)、コンパイルを行わなくてはなりませんでした。
stanでは、記述したモデルをC++にいったん変換し、それからコンパイルして実行することにより、コンパイルされたモジュールに別データを導入して実行することができるようになっています。
さらに、処理スピードも高速化するため、作業の効率化が図れるという利点があります。
stanを使ってベイズ推定を実行してみよう!
重回帰分析について、実際の流れとエクセルを使った実用的な解説をしていきます。
stanを導入しよう!
stanの簡単な導入法として、今回はRを用いたものを紹介します。以下の流れで順を追って説明していきます。
============
①Rのインストール
②Rtoolのインストール
③Rstanのインストール
============
①Rのインストール
まずは、Rのインストール手順について解説します。下記では、Windows環境にインストールすることを前提としています。

CRAN(The Comprehensive R Archive Network)からインストーラをダウンロードします。
「Download R for Windows」をクリックします。

「base」をクリックします。
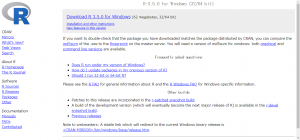
「Download R 3.5.0 for Windows」をクリックします。
ダウンロードした“R-3.5.0-win.exe”を実行します。
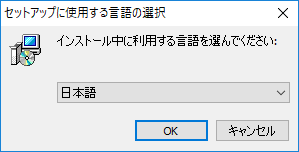
「OK」をクリックします。
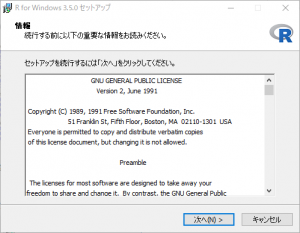
「次へ」をクリックします。
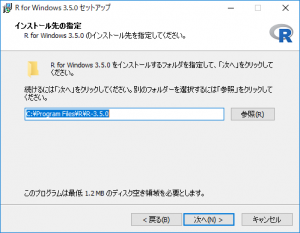
「次へ」をクリックします。
64bit OSのため「32-bit Files」のチェックボックスの選択を外し、「次へ」をクリックします。
「次へ」をクリックします。
「次へ」をクリックします。
「次へ」をクリックします。
②Rtoolsのインストール
Rをインストールしたら、Rtoolsのインストーラをこちらからダウンロードします。Rのバージョンによって、ダウンロードするインストーラが異なります。
今回は、Rのバージョンが3.5.0のため、「Rtools35.exe」をダウンロードし、実行します。
「OK」をクリックします。
「次へ」をクリックします。
「次へ」をクリックします。
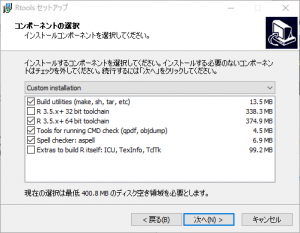
64bitOSのため「32bit toolchain」のチェックボックスを外し、「次へ」をクリックします。
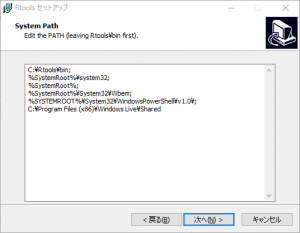
「Add rtools to system PATH」にチェックボックスを入れ、「次へ」をクリックします。
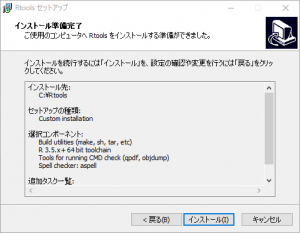
「次へ」をクリックします。
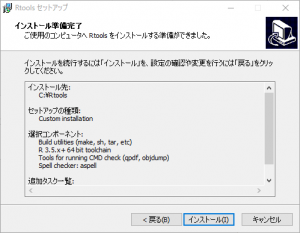
「インストール」をクリックします。
③Rstanのインストール
最後に、Rstanと呼ばれるパッケージをインストールします。
この時、stanも同時にインストールされます。
Windowsメニューから「R x64 3.5.0」を実行します。
コンソール画面が起動します。
コンソールからコマンド「install.packages(“rstan”)」を実行します。
質問が表示されますので、「はい」をクリックします。
ミラーサイトを聞かれますので「Tokyo」を選択し、「OK」をクリックします。
実際にstanを使ってみよう!
ここまででstanの準備が完了しました。ここから実際にstanを使用してベイズ統計を行う方法を紹介します。
①stanを実行するコードを打ち込む。
Rコンソール上から下記コマンドを実行します。
require(rstan)
②統計モデルのコードを打ち込む
Rコンソールに下記コードを入力します。
# モデルの作成
localLevelModel_1 <- ”
data {
int n;
vector[n] Nile;
}
parameters {
real mu; # 確定的レベル(データの平均値)
real<lower=0> sigmaV; # 観測誤差の大きさ
}
model {
for(i in 1:n) {
Nile[i] ~ normal(mu, sqrt(sigmaV));
}
}
“
「vector[n] Nile;」では、ナイル川の流量データが「長さnのデータです。」と宣言しています。
③stanに入れるデータを指定
Rコンソールに下記コードを入力します。
> NileData <- list(Nile = as.numeric(Nile), n=length(Nile))> NileData
$Nile
[1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994
[15] 1020 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100
[29] 774 840 874 694 940 833 701 916 692 1020 1050 969 831 726
[43] 456 824 702 1120 1100 832 764 821 768 845 864 862 698 845
[57] 744 796 1040 759 781 865 845 944 984 897 822 1010 771 676
[71] 649 846 812 742 801 1040 860 874 848 890 744 749 838 1050
[85] 918 986 797 923 975 815 1020 906 901 1170 912 746 919 718
[99] 714 740$n
[1] 100
④ベイズ推定を実行
下記コードを実行します。
# 乱数の種
set.seed(1)# 確定的モデル
NileModel_1 <- stan(
model_code = localLevelModel_1,
data=NileData,
iter=1100,
warmup=10,
thin=1,
chains=3
)
set.seed(1)は、乱数の種です。
モデル式(model_code)には②で作成した「localLevelModel_1」を指定します。データ(data)には③で作成した「NileData」を指定します。
繰り返し回数(iter)は1100回。捨てる個数(warmup)は100回です。データを間引きする間隔(thin)は1に指定しています。1つおきにデータを使用するということは全部のデータを使うということです。シミュレーションを繰り返す回数(chains)は3回としています。
⑤推定がうまくいったかを確認
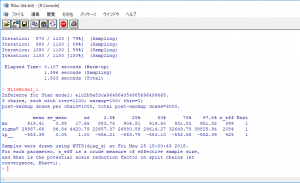
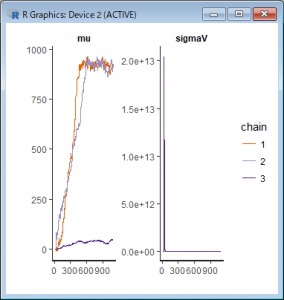
下記コマンドをRコンソールから実行し、プロットします。
> # 計算の過程を図示
> traceplot(NileModel_1)
すると、グラフの最初の方において値がおかしくなっているのがわかります。
warmupが少なかったため、10から100に増やして実行してプロットしたところ、以下のようになりました。
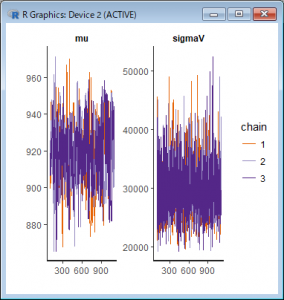
⑥実行結果から言えることを確認
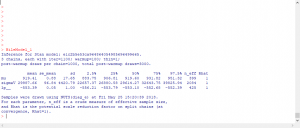
パラメータmuの行で、mean列に919.41とあります。これは「多く生成されたパラメータmuの平均値」です。他には「多く生成されたパラメータmuの標準偏差」や95%区間などが載っています。
パラメータの95%区間が出ていますが、これは「パラメータmuが883.75から951.32の間にある確率が95%である。」という意味です。
ベイズ統計の有用性とstanの優位性
ビジネスやマーケティングなどの実生活でもベイズ統計は応用されています。
例えば、ロケットの軌道を推定する、創薬時にたんぱく質の構造を解析する場合などです。
近年の情報社会において、得られたビッグデータから推測される事象を推定することを可能にするベイズ推定は、非常に有効なツールです。
Googleの検索エンジンや自動で迷惑メールフォルダに新規メールを送り込む技術にも使用されており、今後、使用用途はさらに拡大していくと考えられます。
こういった点を踏まえると、統計ソフトのRや統計用ライブラリを多く持つPythonよりも高速でベイズ推定を可能にするstanは優位性があると言えます。
本記事を参考に操作を行うことで、ベイズ推定をすることができ、結果が出すところまではできます。
しかし、それらの値の意味を理解するためには最低限の統計学の知識が必要である点は留意が必要です。













最新情報・キャンペーン情報発信中