箱ひげ図の概念から作り方まで、わかりやすく解説！

データの「ばらつき」からは、その環境や条件における重要なヒントが隠されています。ばらつきを探る指標としては「ヒストグラム」が普及していますが、「箱ひげ図」も非常に有用性の高い手法です。

2012年に改訂された新学習指導要領では、新たに「高校数学Ⅰ」の科目としてこの「箱ひげ図」が追加されました。データ分析の現場でも、少しずつスタンダードになっていくかもしれません。

こちらでは、「箱ひげ図」の概念や、作成方法、活用方法などについてお話します。

箱ひげ図の見方

箱ひげ図は、その名のとおり「箱」と「ひげ」によって構成される、データのばらつきを可視化するための図式です。「棒グラフ」「円グラフ」「折れ線グラフ」「散布図」「ヒストグラム」と同様に、データの分布を確認する手法のひとつとして活用されています。

統計における分析方法の中でも、比較的簡単にデータのばらつきを把握できるのが箱ひげ図の魅力です。また、データの集合体ごとに箱ひげ図を描くことで、各データのばらつきを調べることもできます。

以下は箱ひげ図を理解する上で重要な5つの概念です。

中央値

データにおける「真ん中」の値です。具体的には、データを小さい順（大きい順）に並べた際に、中央に位置する値を意味します。詳細は後述しますが、データの合計をデータの個数で割る「平均値」とはまったく性質が違う値です。

四分位数

四分位数とは、データを小さい順（大きい順）に並べ、四等分した際の区切りの値を指します。全体で25％の場所に位置する値を「第1四分位数」、75％の場所に位置する値を「第3四分位数」と呼びます。上述した中央値は「第2四分位数」にあたる値です。

四分位範囲

第1四分位数と第3四分位数の間の範囲を「四分位範囲」と呼びます。箱ひげ図では、箱の上辺・底辺間の範囲が四分位範囲に該当します。

最小値（最大値）

箱ひげ図ではデータにおける最小値（最大値）もグラフ上に表記します。「ひげ」の上端・下端がそれぞれ最大値・最小値です。

外れ値（特異点）

データの中で突出した値は、「外れ値（特異点）」として扱います。箱ひげ図では外れ値をひげに含めず、独立した値として点で表記します。

図1は一般的な箱ひげ図の形です。

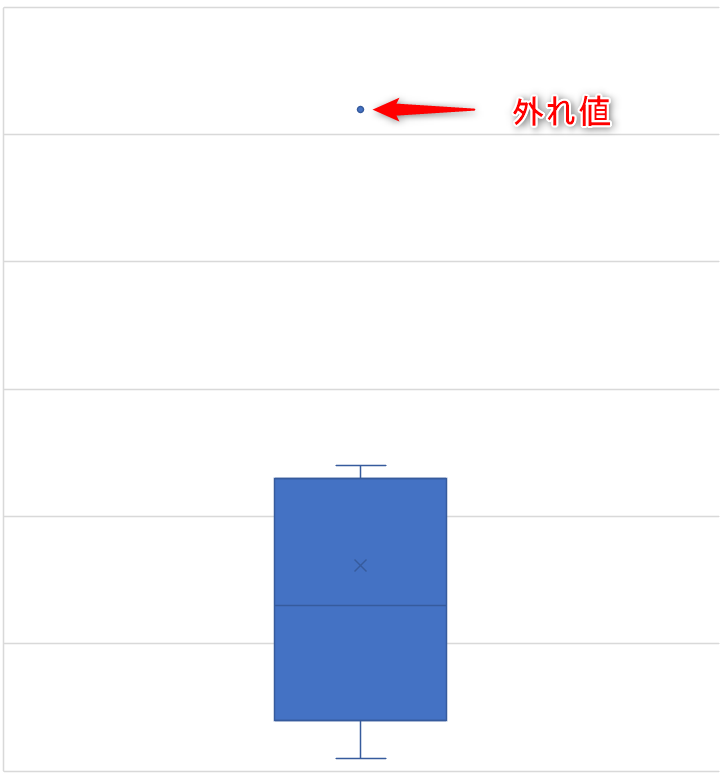
外れ値がある場合、箱ひげ図は図2のような形になります。

図１

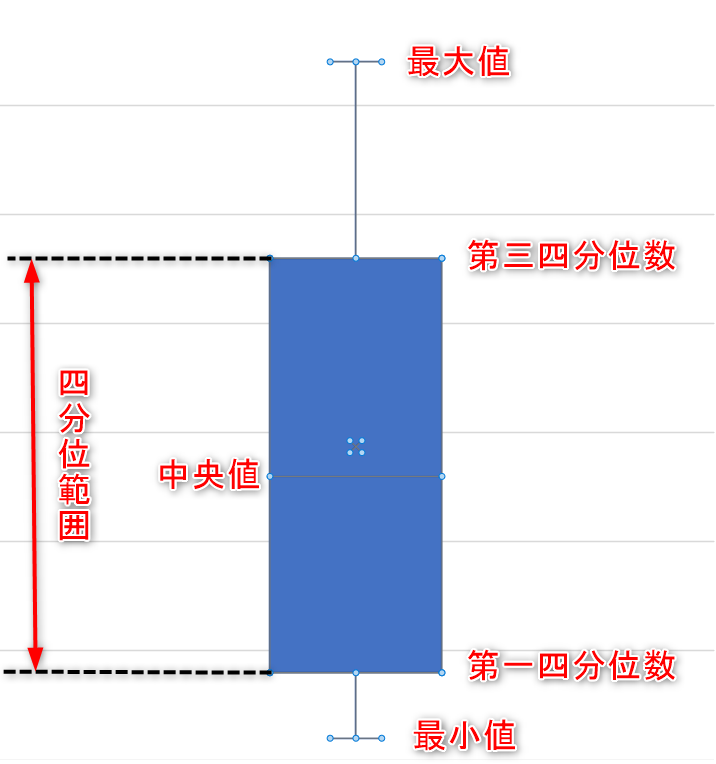
図２

どうして箱ひげ図を使うの？

データのばらつきを表現する手法は複数存在します。その中で、箱ひげ図をチョイスするメリットはどこにあるのでしょうか。

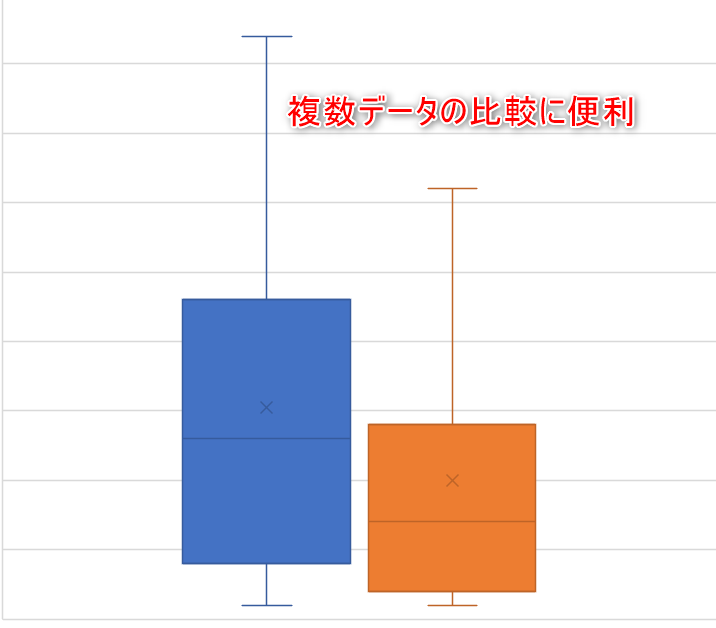
ひとつは、複数のデータ（母集団）を同時に扱える点です。同じくデータのばらつきを可視化するヒストグラムで扱えるのは、原則としてひとつのデータのみ。箱ひげ図は図3のように、複数データのばらつきを並べて比較するために重宝します。

図３

もうひとつは、平均値ではなく中央値を用いることで、「実質的」なデータの「真ん中」を表現できる点です。平均値はデータの「真ん中」を算出する手法として広く普及している一方で、集団から突出している数値が存在するとその数値に「引っ張られて」しまうという欠点を有しています。

例えば、［1,2,3,4,5,6,7,8,9,10,100］というデータの平均値は約14.1になりますが、この数値は必ずしもデータの「真ん中」を示しているとは言えません。箱ひげ図の概念においてこのデータの中央値は6となり、100は除外して考えるべき外れ値として扱われます。

図4を見ていただければ、平均値と中央値のどちらが「実質的」なデータの「真ん中」を表しているかがおわかりいただけるかと思います。

図4

箱ひげ図の作り方を紹介します！

ここまでで、箱ひげ図の簡単な概念についてはおわかりいただけたかと思います。ここからは、実際に箱ひげ図を制作してみましょう。実際の計算手順と、エクセル2016を活用した簡単な方法についてご説明します。

箱ひげ図を作るまでの流れ

箱ひげ図を作成する際は、中央値や各四分位数を算出していくことになります。

①最初に算出しなければならないのは中央値です。

データに含まれる数値の個数が奇数の場合、数値の大きさで並べたときに真ん中に位置する数値が中央値です。偶数の場合は、真ん中の位置している2つ数値の平均値を中央値として扱います。グラフには箱の中の横線として、中央値の線を引きましょう。

②③四分位範囲については、上述した行程で算出した中央値より大きい値・小さい値に限定した範囲での「中央値」として考えます。中央値の考え方は、上述した方法と同じです。この算出により、箱の上辺・底辺として記入する第1四分位数・第3四分位数が割り出されます。ここまでの行程で「箱」は完成です。

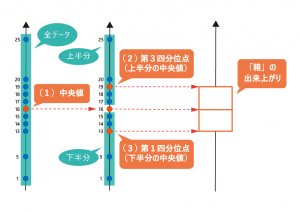
ここからは「ひげ」を描く行程に入りますが、まず「外れ値」を定義する必要があります。

④⑤第1四分位点と第3四分位点の間（四分位範囲）の長さを求め、箱の上下端からその長さの1.5倍をとった範囲を把握しましょう。

⑥その範囲より外側にある数値を外れ値として扱い、点を記入します。外れ値がない場合は、特に点を打つ必要はありません。

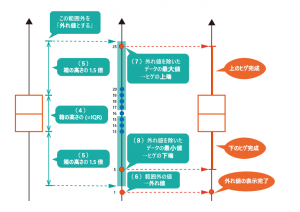
⑦⑧外れ値を除外した最大値と最小値に線を引き、上下の「ひげ」を完成させます。最後に全データの平均値を算出し、印を記入して完成です。

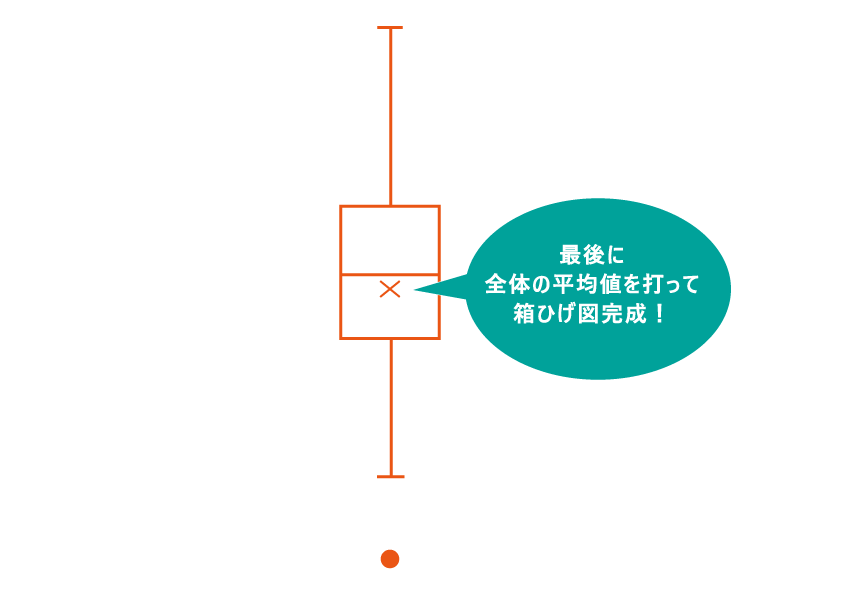
箱ひげ図をエクセルで作ってみよう！

上述した行程で箱ひげ図を１から完成させるのは、手間がかかってしまうかもしれません。エクセルには2016から簡単に箱ひげ図を作成できる機能が実装されました。その方法を手順に添ってご説明しましょう。

まず、箱ひげ図のもととなるデータを入力します。

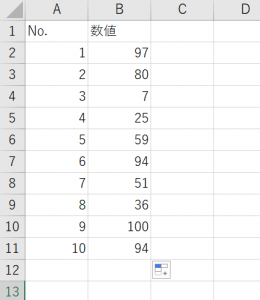
次に箱ひげ図に反映させる数値を範囲選択します。

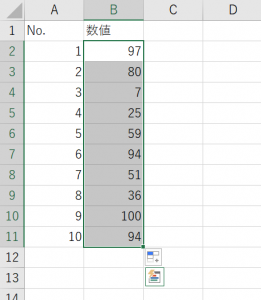
範囲選択した状態で、タブから1.［挿入］→2.［統計グラフの挿入］→3.［箱ひげ図］を選択してください。

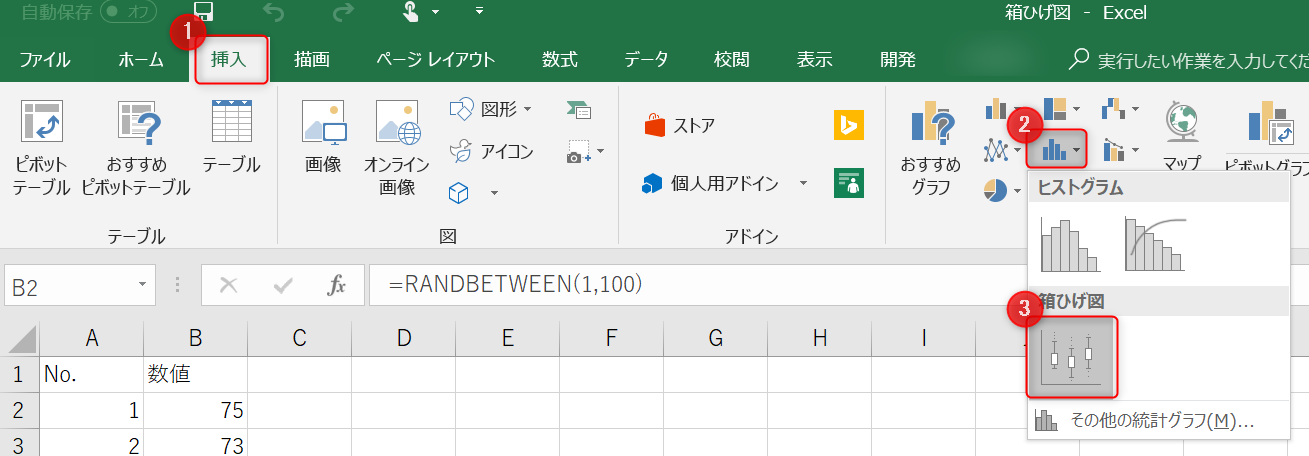
選択した数値に応じた箱ひげ図が出力されます。タイトルを編集することも可能です。

箱の部分にポインタを合わせ右クリックし、［データ系列の書式設定］をクリックすると必要に応じて表示する項目を変更できます。

「内側のポイントを表示する」にチェックを入れると、外れ値以外の数値も点で表示されます。

［特異ポイント］を表示するは、外れ値表示の有無を決める項目です。デフォルトではチェックが入っています。

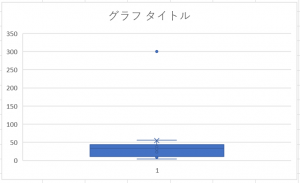
平均値の点が必要ない場合は［平均マーカーを表示する］のチェックを外しましょう。

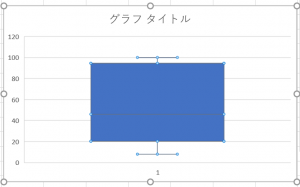
同系列で複数の数値がある場合に［平均線を表示］にチェックを入れると、各平均値が折れ線グラフで結ばれます。

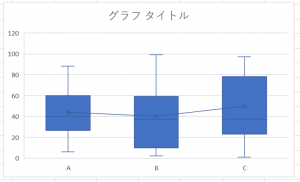
［排他的な中央値］［包括的な中央値］は第1四分位数・第3四分位数の決定に影響します。

上述したとおり、第1四分位数と第3四分位数はどちらも、中央値を起点として下半分（上半分）の中央値です。［包括的な中央値］にチェックを入れると、中央値を含めた下半分（上半分）で、第1四分位数と第3四分位数を決定します。

対して「排他的な中央値」にチェックを入れると、中央値は計算から除外されます。それぞれは箱の上辺・底辺の位置に影響を与える選択項目ですが、図の制作のもととなる数値の個数が多いほど、双方の差異は小さくなります。

箱ひげ図をデータ分析に活かそう！

「ビッグデータ」という概念が普及した現在、あらゆる業態において膨大に蓄積されているデータの有用性が探られています。

とりわけデータの「ばらつき」を把握することは重要であり、直感的にビジュアライゼーションできる方法がビジネスでは求められるでしょう。箱ひげ図はそうしたビジネスにおけるデータ分析に便利な表現方法です。

代表的な活用例は売上のばらつき把握です。突出した外れ値に引っ張られず数値の真ん中を把握できる箱ひげ図であれば、平均値よりも「実質的」な店舗や企業の現状を把握できます。複数店舗や支店の売上のばらつきを並べて把握することも容易です。

売上に関して言えば、中央値に対する第1四分位数の差が小さく、第3四分位数が高い状態において良い結果が出ていると言えます。複数条件での売上の箱ひげ図を比べることで、その商品に最も適した条件を見定めることもできるでしょう。

一方で、箱ひげ図を最大限活用して分析に活かすためには、最低限の統計知識は必要です。ヒストグラム、箱ひげ図など分析の手法はあくまでツールにすぎず、応用していくためには使う側に統計という概念への理解が求められます。

今回ご紹介した箱ひげ図を活用すれば、数値のばらつきを簡単に可視化できます。

より統計へに理解を深めるために、Udemyのオンライン動画講座を活用してみてください。

Udemyでは、数式を使って統計を学べる講座も数多く用意しています。

これを機に、データサイエンス・統計を学んでみてはいかがですか？