【ロジスティック回帰分析】使用例やオッズ比、エクセルでの使い方も紹介！

統計を使用すれば、事象の発生を予測・説明することも可能です。

x1、x2……と複数の要因が考えられる場合、「ロジスティック回帰分析」を用いてyという特定の事象が起こる確率を検討できます。

こちらでは、ロジスティック回帰分析の使用例、オッズ比、エクセルでの実施方法についてお話します。

公開日：2018年8月29日

ロジスティック回帰分析とは？いつ使うの？

ロジスティック回帰分析とは、複数の変数から分析を行う「多変量解析」の一種であり、質的確率を予測します。

簡単に言えば、ある因子から判明していない結果を予測するため、あるいは既に出ている結果を説明するために用いられる関係式です。

関係式は、現象の要因である「説明変数（x1、x2、x3…）」と、現象を数値化した「目的変数（y）」で構成されています。y=が1に近いほど、その事象が起きる確率は高いことを意味します。

ロジスティック回帰分析の活用例は？

ロクスティック回帰分析は、「ある事象の発生率」を判別する分析です。このことから、さまざまなシーンでの活用が期待できます。

DMへの返信を「事象」と定義すれば、そのキャンペーンの反応率がわかります。「顧客による特定商品の購入」を「事象」と考えるのも一般的です。このほか、マーケティングの分野では広く活用されています。

また、気象観測データからの土砂災害発生予測、患者の検査値から病気の発生率を予測するなど、危機回避のために活用されることも少なくありません。金融系のリスクを知るために活用しているアナリストもいるようです。

わかりやすいモデルとして、アルコール摂取量・喫煙本数からとがん発症の有無（有=1、無=0）の関係性を調べるケースを想定してみましょう。

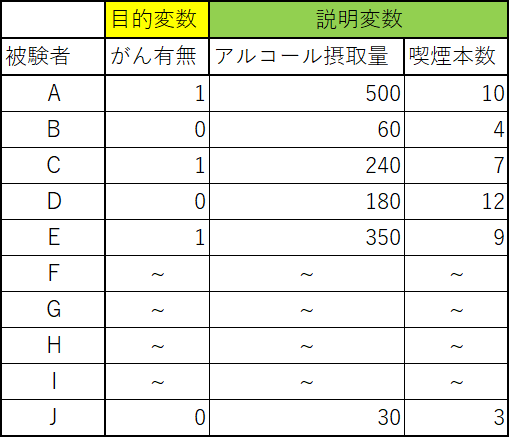
ロジスティック関数に1日あたりのアルコール摂取量（ml）と喫煙本数を当てはめ、がん発症の有無との相関関係がわかれば、アルコール摂取量と喫煙本数から発見されていないがん発症を予測できます。

重回帰分析とロジスティック回帰分析の違いとは？

ロジスティック回帰分析と重回帰分析はともに回帰分析の手法であり、どちらも複数の説明変数とひとつの目的変数（従属変数）を取り扱います。両者の違いについてお話しましょう。

重回帰分析では、説明変数xが目的変数yの値を変化させます。そのため、説明変数から、目的変数の「値」を予測可能です。

一方、ロジスティック回帰分析で考えるのは「特定の現象の有無」であり、yが1になる確率を判別します。事象の有無がはっきりと決まる場合に重回帰分析を用いても、期待する結果は得られないので、注意しましょう。

ロジスティック回帰分析の実際の計算方法は？

今度は、ロジスティック回帰分析を実際に計算してみましょう。

確率については、以下の計算式で算出できます。

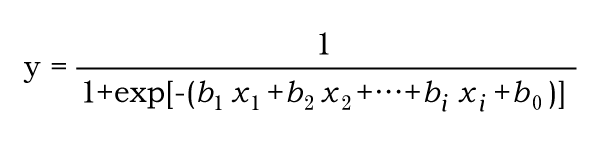
biは偏回帰係数と呼ばれる数値です。xiにはそれぞれの説明変数が代入されます。

biは最尤法（さいゆうほう）という方法で求めることができます。統計ソフトの「R」を用いるのも一般的です。

「R」については「【R言語入門】統計学に必須な“R言語“について1から解説！」の記事を参照してください。

ロジスティック回帰分析の見方

式で求められるのは、事象が起こる確率を示す「判別スコア」です。

上述したモデルを例にすると、アルコール摂取量と喫煙本数からがんを発症している確率が算出されます。判別スコアの値は以下のようなイメージです。

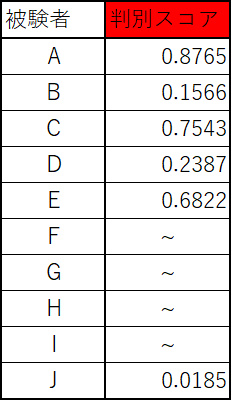
Aの被験者を例にすると、87.65％の確率でがんを発症しているということになります。

オッズ比とは

上述した式においてyは「事象が起こる確率」です。一方、「事象が起こらない確率」は（1-y）で表されます。「起きる確率（y）」と「起こらない確率（1-y）」の比を「オッズ」といい、確率と同様に事象が起こる確実性を表します。

その事象がめったに起こらない場合、yが非常に小さくなると同時に（1-y）も1に近似していきます。この場合、確率をオッズは極めて近い値になるのです。

オッズが活用されている代表的なシーンがギャンブルです。例として競馬では、オッズをもとに的中した場合の倍率が決定されています。

また、オッズを利用すれば各説明変が目的変数に与える影響力を調べることが可能です。

ひとつの説明変数が異なる場合の2つのオッズの比は「オッズ比」と呼ばれており、目的変数の影響力を示す指標です。オッズ比の値が大きいほど、その説明変数によって目的変数が大きく変動することを意味します。

ロジスティック回帰分析のやり方！エクセルでできる？

最後に、ロジスティック回帰分析のやり方を紹介しましょう。

ロジスティック回帰分析には、主にエクセル、R、統計解析ソフト「SPSS」を使用する方法があります。SPSSは購入が必要であり、Rも初心者の方が使うには多少ハードルが高いソフトウェアです。ロジスティック回帰分析をする際、最も一般的なのは、エクセルを使った方法でしょう。

エクセルでロジスティック回帰分析を行う場合には、まず、SUMPRODUCT関数で偏回帰係数の初期値を0とした場合の推定値を求めます。

続いて、LN関数を使用してデータごとの対数尤度（ゆうど）を算出しましょう。最終的な対数尤度はSUM関数で求められます。

最後にエクセルの「ソルバー」という機能を使用します。「目的セルの設定」というボックスで対数尤度のセルを選択し、「変更セルの変更」ボックスには偏回帰係数の初期値０を入力していたセルを範囲選択してください。

「目標値」として最小値を選択、「解決方法の選択」では「GRG非線形」を選んでください。「成約のない変数を非負数にする」のボックスにチェックが入っている場合は、チェックを外しましょう。

最後に解決をクリックすれば、各変数の偏回帰係数ならびに、目的変数が1になる確率が出力されます。

事象の発生確率を明確に把握できるロジスティック回帰分析。マーケティングでの応用が多いのはお伝えしたとおりですが、その有用性から医療現場や、ひいては心理学の現場で使われることも珍しくありません。

評価：★★★★★
機械学習の実装に向けて、基礎からデータを使った実装に向けて順次説明していただきました。注意点なども含めて説明いただいたので理解しやすかったです。データを使ったPythonのモデル構築は難しかったですが、進め方考え方がわかりました。

評価：★★★★★
ものの考え方を客観的に概念として理解することができた