Excelを使ったデータ分析の機能ごとの使い方・活用法を解説

Excelでデータ分析が行えること自体は知っているものの、

具体的なやり方が分からない…。
どこまで分析ができるか知りたい…。

という方もいるのではないでしょうか。
Excelにはデータ分析機能と呼ばれるアドインがあり、簡単にデータ分析を始められます。この記事では、

Excelでデータ分析を行う際の設定や導入方法
Excelのデータ分析でできることや機能の使い方

について解説します。

Excelの「データ分析機能」の活用の幅

Excelの分析ツールは直感的な操作で使えるため、初心者にも扱いやすいです。PythonやR言語などのプログラミング知識を学ばなくても、平均値や回帰分析などのデータ分析を行えます。

また、導入も簡単なため、手間や学習コストを抑えて実務的な分析を始められることがExcelのデータ分析機能の特徴です。具体的な機能や使い方については後述の「Excelの「データ分析」でできること・各機能の使い方」をご覧ください。

Excelの「データ分析」の基本：設定・導入方法

Excelのデータ分析機能を使う際は、オプション画面から「アドイン管理画面」を開き、「分析ツール」を有効に設定します。導入方法は以下の3ステップです。

1. Excelのオプション画面を開く
2. アドイン管理画面へ進む
3. 分析ツールを有効にする

ここからは、以下の環境のもと各工程について具体的に解説します。

OS：Windows11 Excel：Microsoft365 Excelバージョン2509

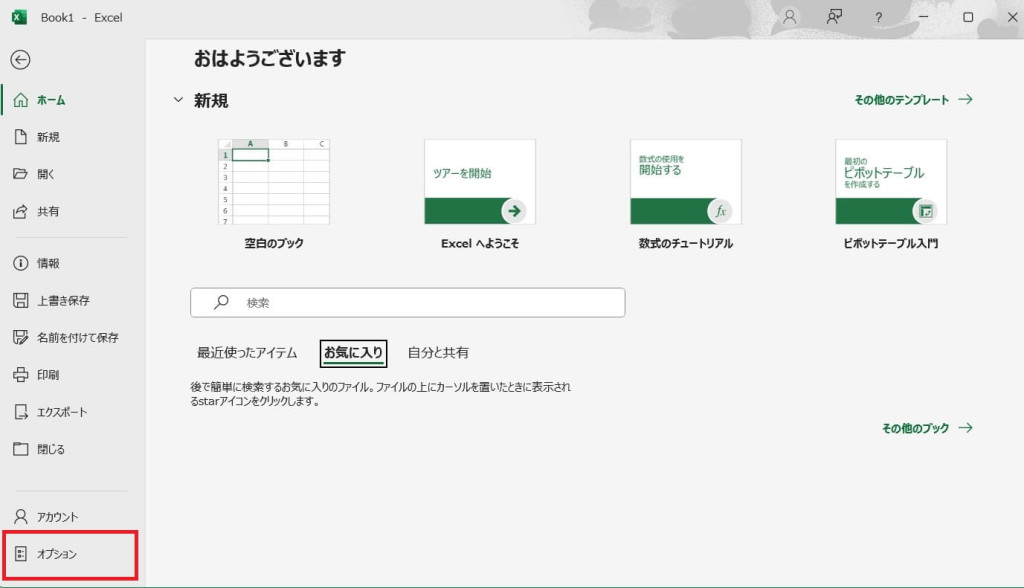
Excelのオプション画面を開く

Excelを開き、画面左上の「ファイル」タブをクリックします。

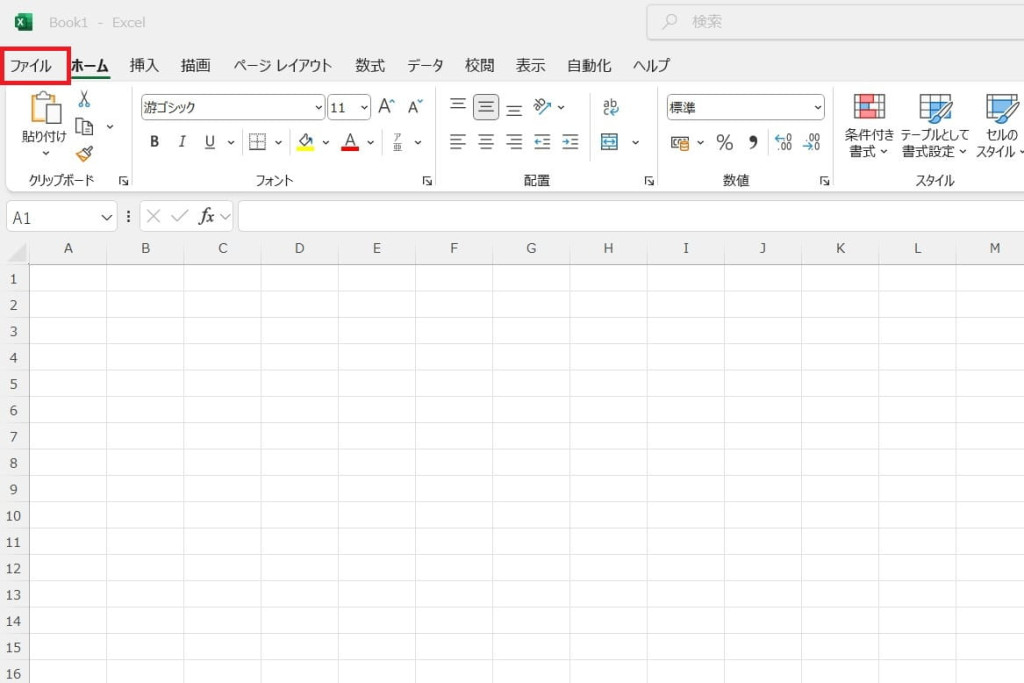
表示されたメニューの一番下にある「オプション」をクリックします。

アドイン管理画面へ進む

Excelのオプション画面の左側メニューから「アドイン」をクリックします。

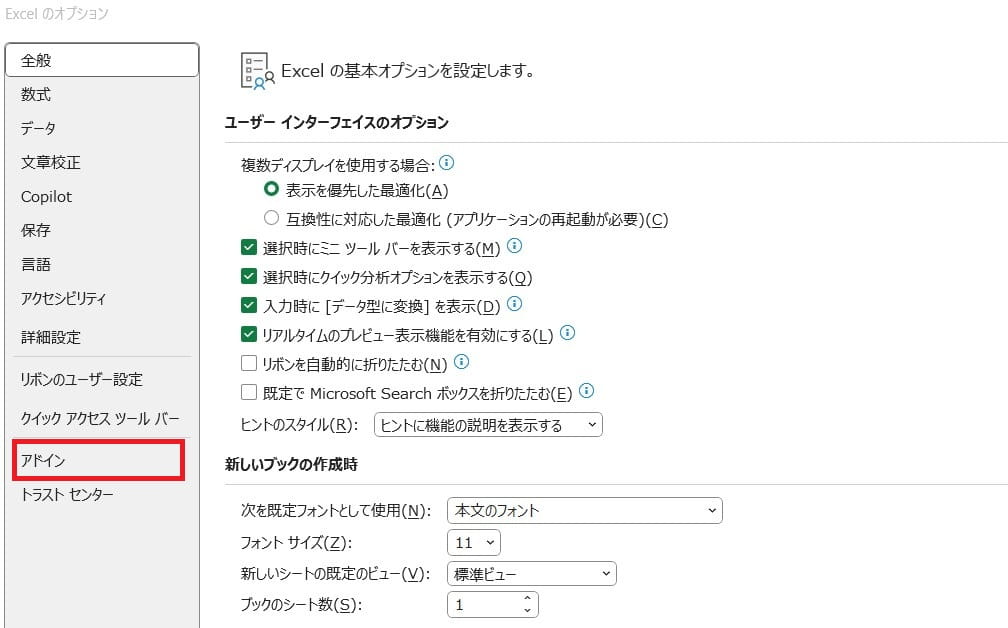
ウィンドウの下部にある「管理(A)というドロップダウンリストが「Excelアドイン」になっていることを確認します。

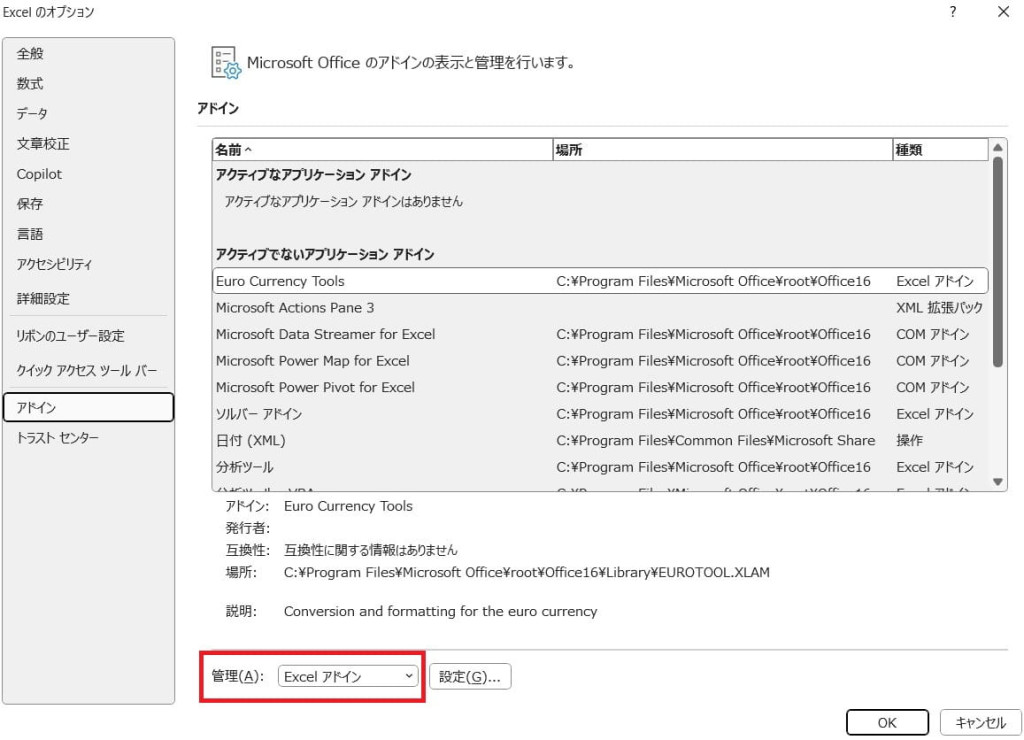
「設定…」ボタンをクリックします。

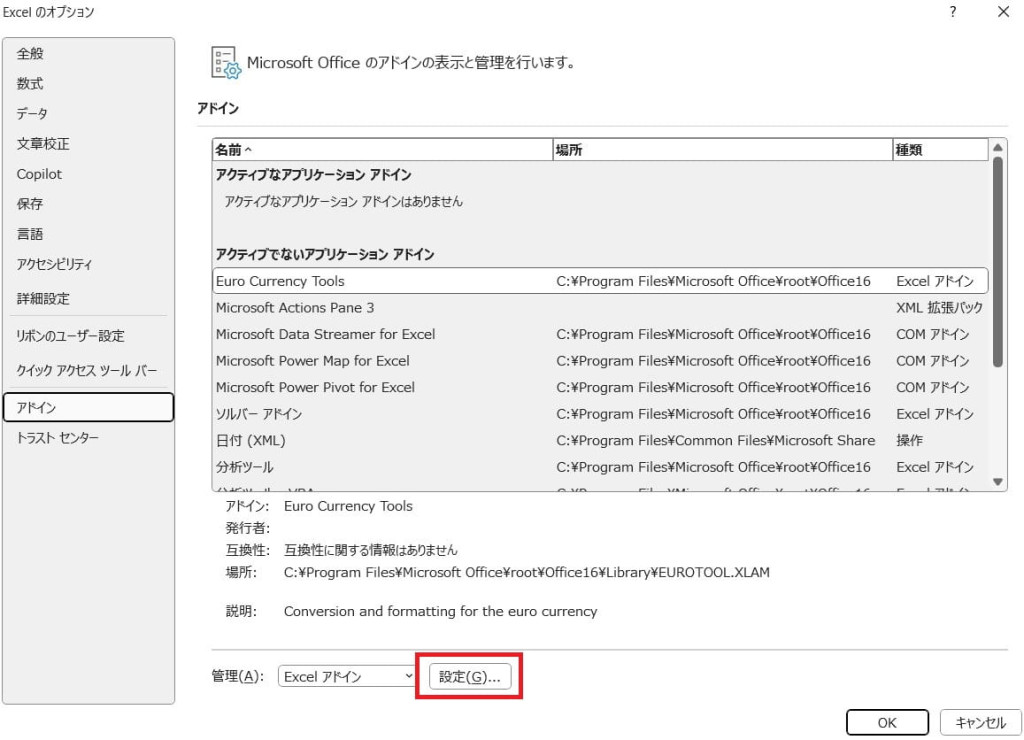
分析ツールを有効にする

「アドイン」ウィンドウに表示される、利用可能なアドインの一覧から「分析ツール」を探し、チェックボックスにチェックを入れます。

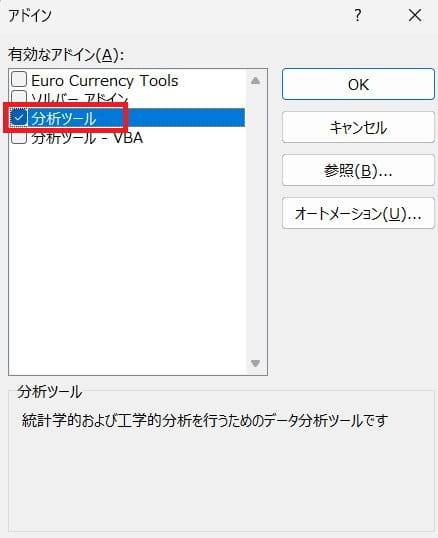
「OK」ボタンをクリックしてウィンドウを閉じれば、データ分析機能を使うための準備は完了です。

以上で基本の設定が完了したので、分析したいときはリボンメニューの「データ」タブから「データ分析」ツールを呼び出せるようになります。

Excelの「データ分析」でできること・各機能の使い方

「データ分析」機能は、以下の表に記載がある統計手法などを使って、データを分析できるExcelの拡張機能です。準備コストが少なく操作がシンプルなため、初心者でもデータ分析に取り組めます。

【データの全体像・分布をつかむ（要約・可視化）】

• 基本統計量
• ヒストグラム
• 順位と百分位数
  
  【時系列の傾向をつかむ（平滑化・周期）】
• 移動平均
• 指数平滑
• フーリエ解析
  
  【変数同士の関係を知る（関連・予測）】
• 相関
• 共分散
• 回帰分析
  
  【差があるか確かめる（検定）】
• t検定（一対の標本による平均の検定）
• t検定（等分散を仮定した2標本による検定）
• t検定（分散が等しくないと仮定した2標本による検定）
• z検定（2標本による平均の検定）
• F検定（2標本を使った分散の検定）
• 分散分析（一元配置）
• 分散分析（繰り返しある二元配置）
• 分散分析（繰り返しない二元配置）
  
  【データを用意する（生成・抽出）】
• 乱数発生
• サンプリング

ここからは、データ分析機能の使い方について解説します。

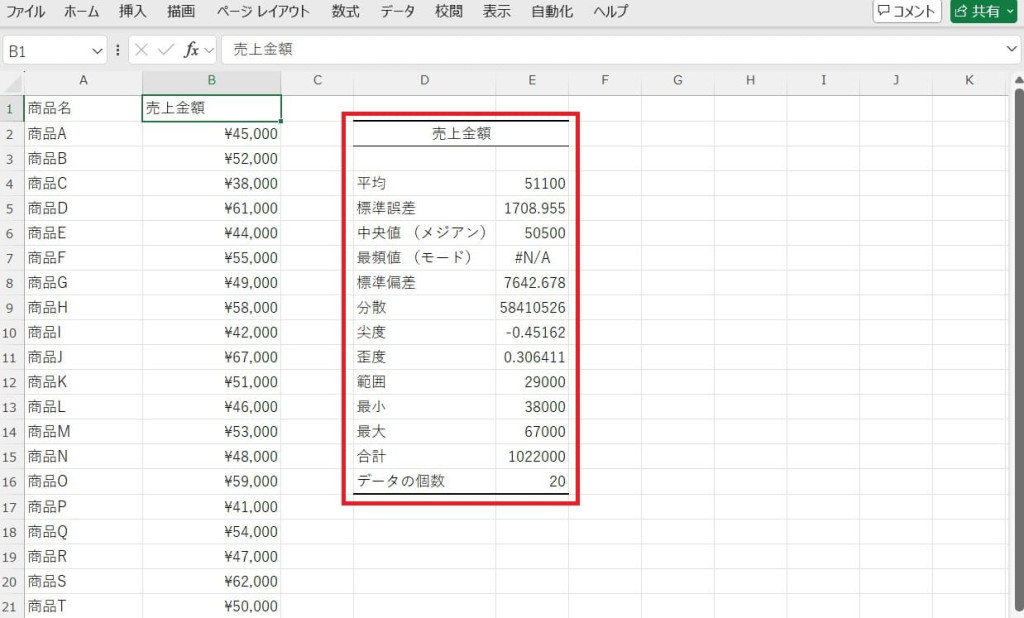
基本統計量

平均や中央値、標準偏差、最大値、最小値といった基本的な統計量を計算できます。データの分布や傾向を把握し、データの特性を前準備として利用可能です。

【基本統計量の使い方】

データを列形式で入力します。

メニューの「データ分析」から「基本統計量」を指定します。

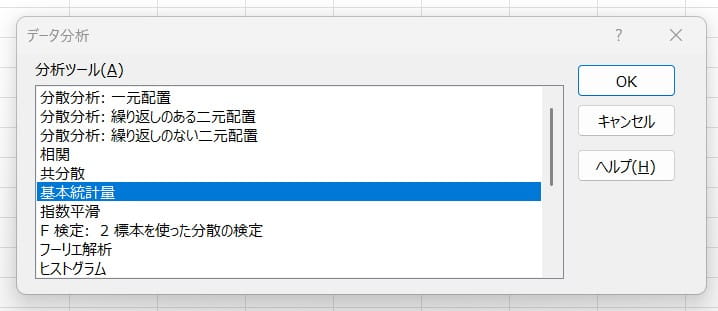
入力範囲や出力範囲などを設定します。

基本統計量が出力されました。

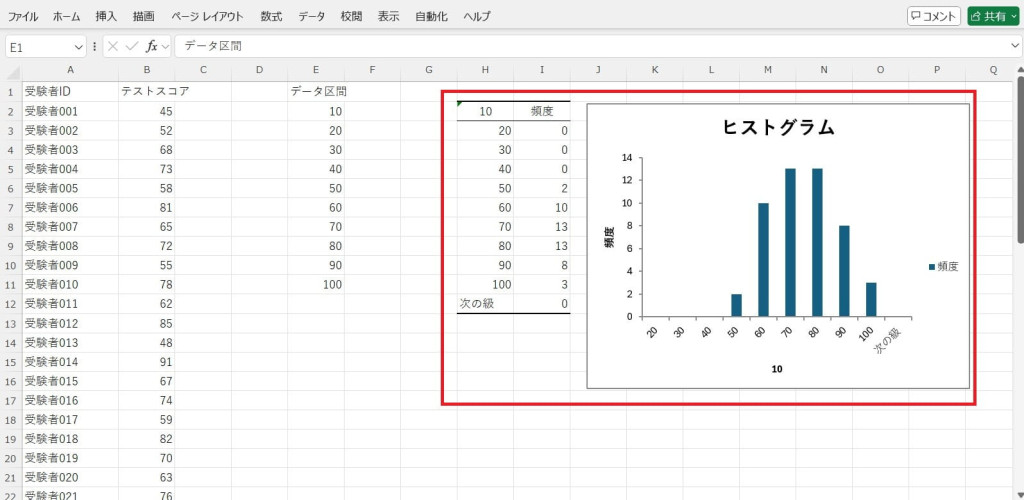
ヒストグラム

データの頻度分布をグラフとして表し、データの偏りや形状を視覚的に把握できる機能です。どのような値のデータが多いかなど、統計的な傾向を理解するために役立ちます。

【ヒストグラムの使い方】

データを列形式で入力します。

「データ分析」ツールでヒストグラムを選択します。

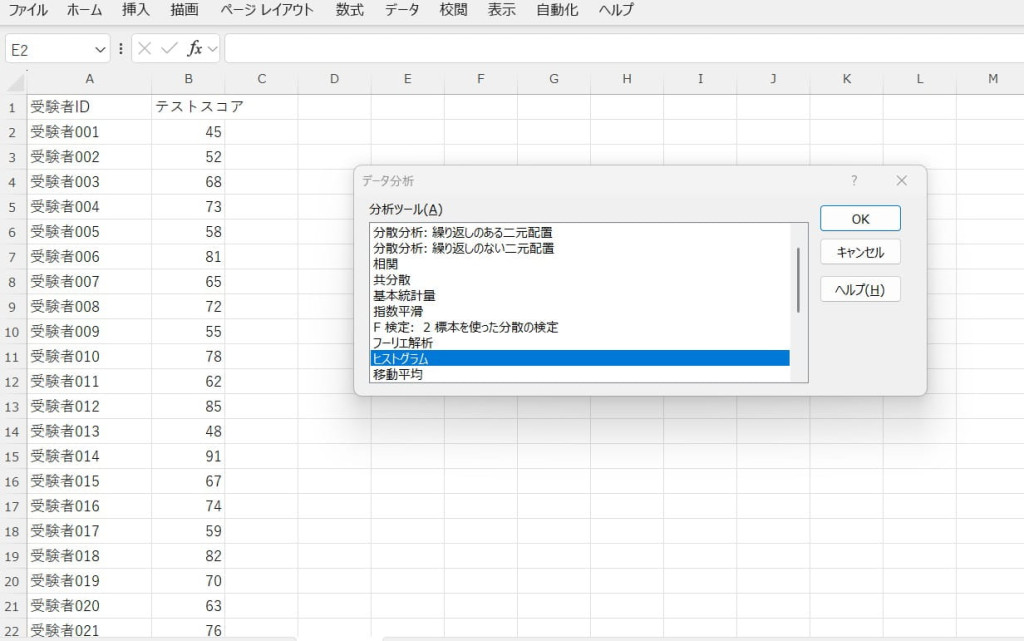
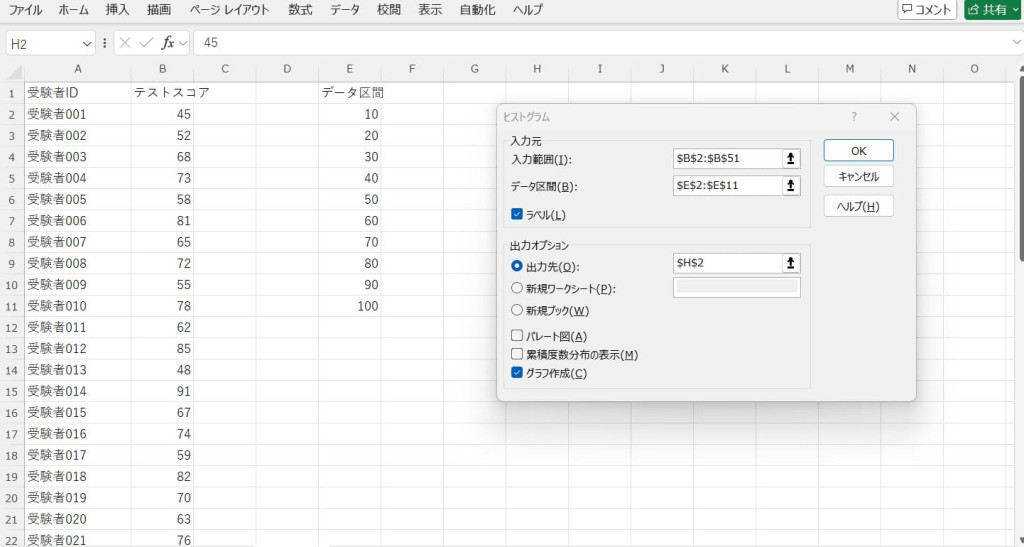
入力範囲やデータ区間などを設定します。

ヒストグラムが表示されました。

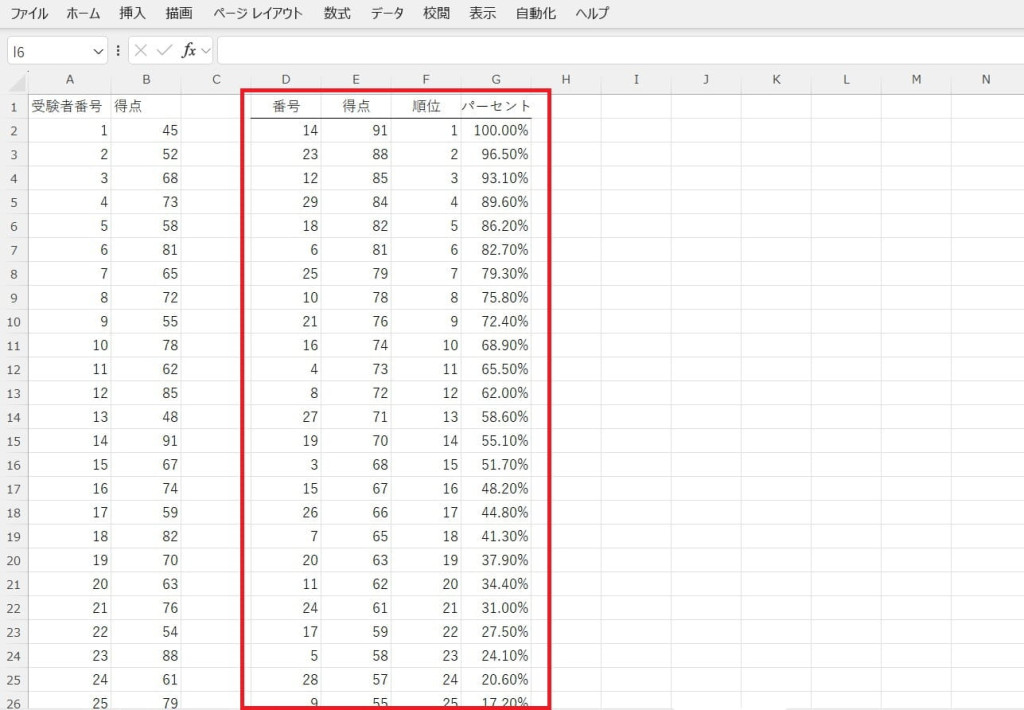
順位と百分位数

データの順位や百分位数を計算し、個々のデータが全体の中でどの位置にあるかを分析できます。試験結果やマーケティング分析などで、データの偏りや分布を把握するために応用可能です。

【順位と百分位数の使い方】

データを列形式で入力します。

データ分析から「順位と百分位数」を選択します。

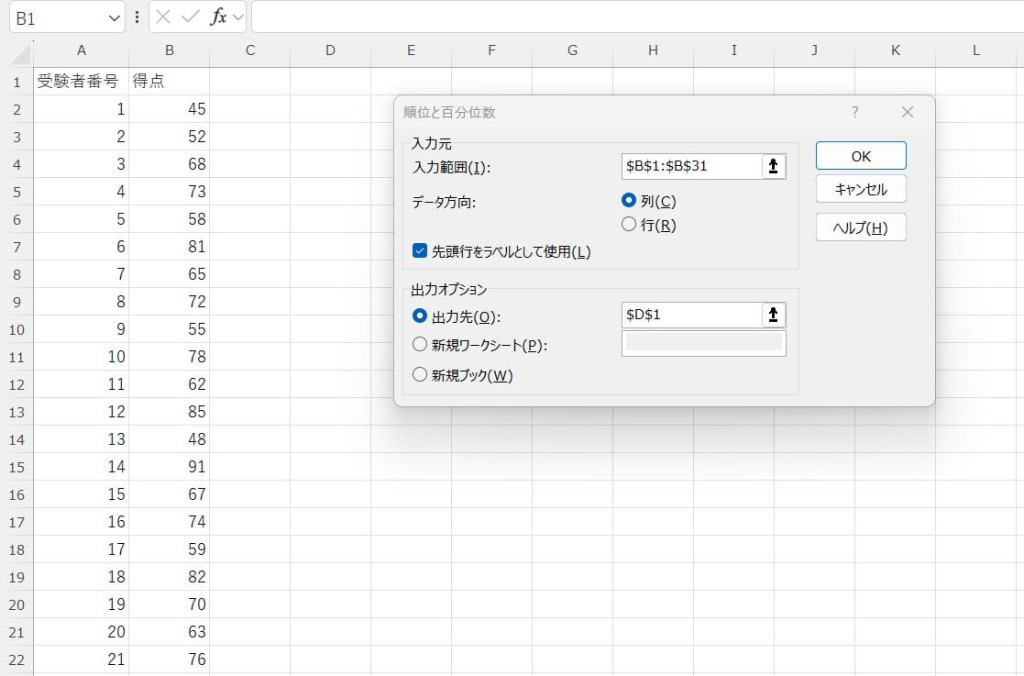
順位や百分位数を計算する対象範囲、出力先などを指定します。

結果を確認し、データの位置づけを評価します。

移動平均

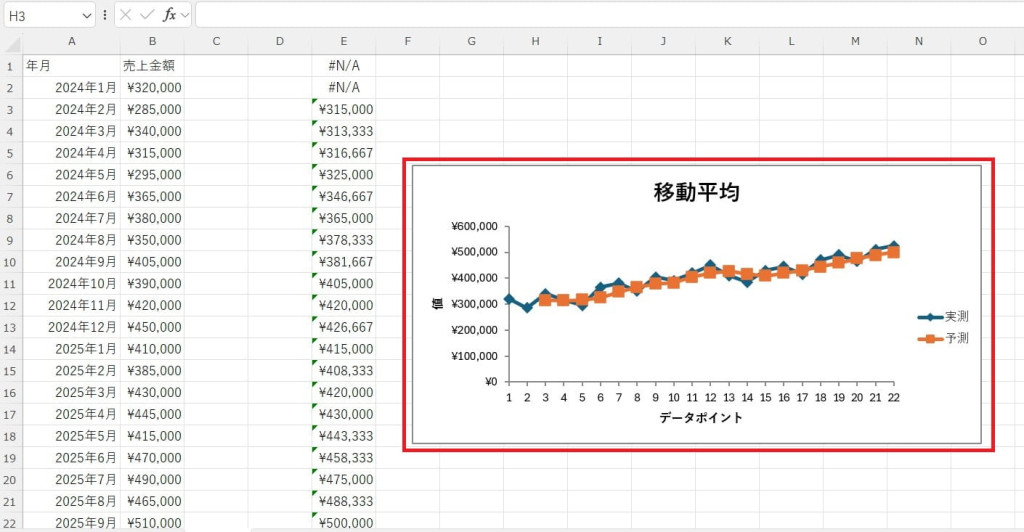
移動平均は、時系列データの変動を滑らかにし、傾向を明確化する分析手法です。データ内のノイズを除去することで、短期的なトレンドや季節変動を把握しやすくなります。また、売上予測や市場動向分析に効果的です。

移動平均を活用すれば、変動の背景にあるトレンドを容易に読み取れます。

【移動平均の使い方】

時系列データを列形式で入力します。

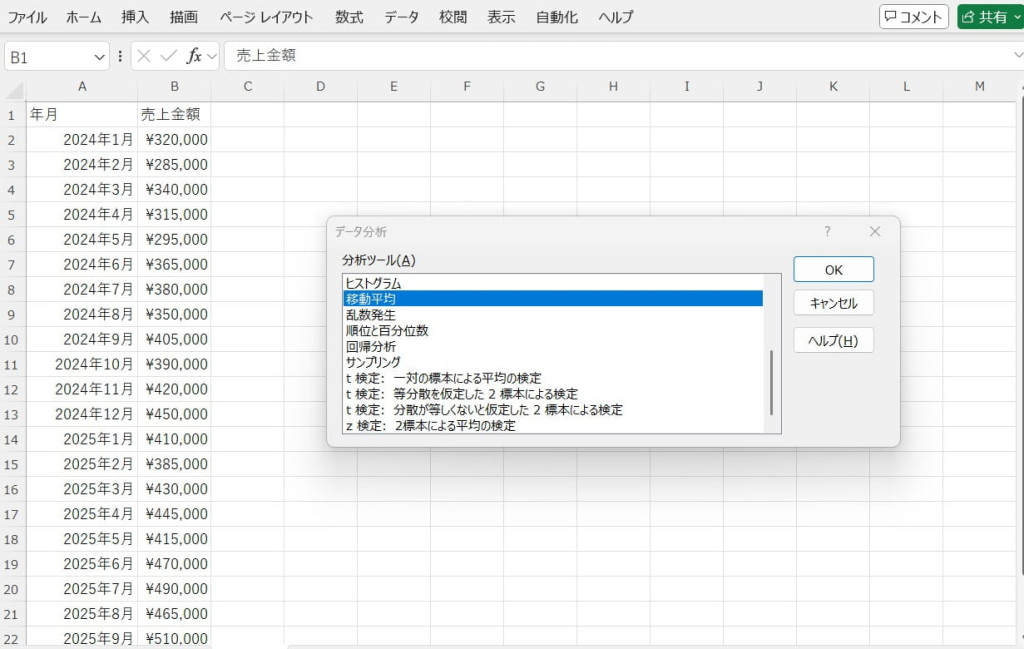
「データ分析」ツールで移動平均を選択します。

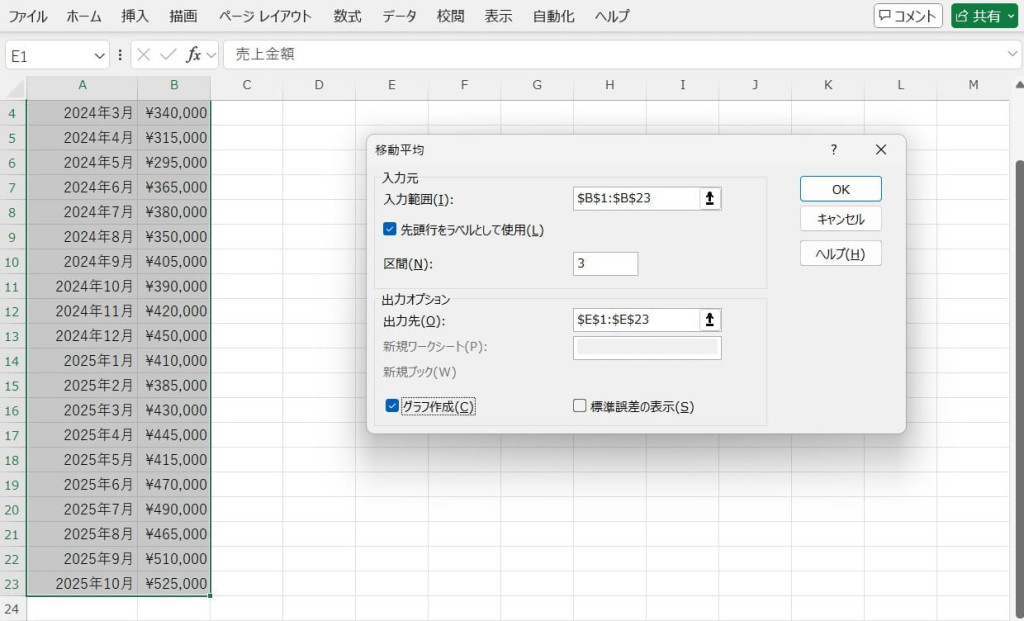
入力範囲や平均を計算する区間、出力先などを指定します。

平滑化されたデータを確認し、傾向を分析します。

指数平滑

時系列データの変動を平滑化する機能です。データのノイズを減らし、トレンドを明確化することで、短期的なデータの予測に活用できます。売上予測や在庫管理などに応用できる分析手法です。

【指数平滑の使い方】

時系列データを入力します。

「データ分析」ツールで指数平滑を選択します。

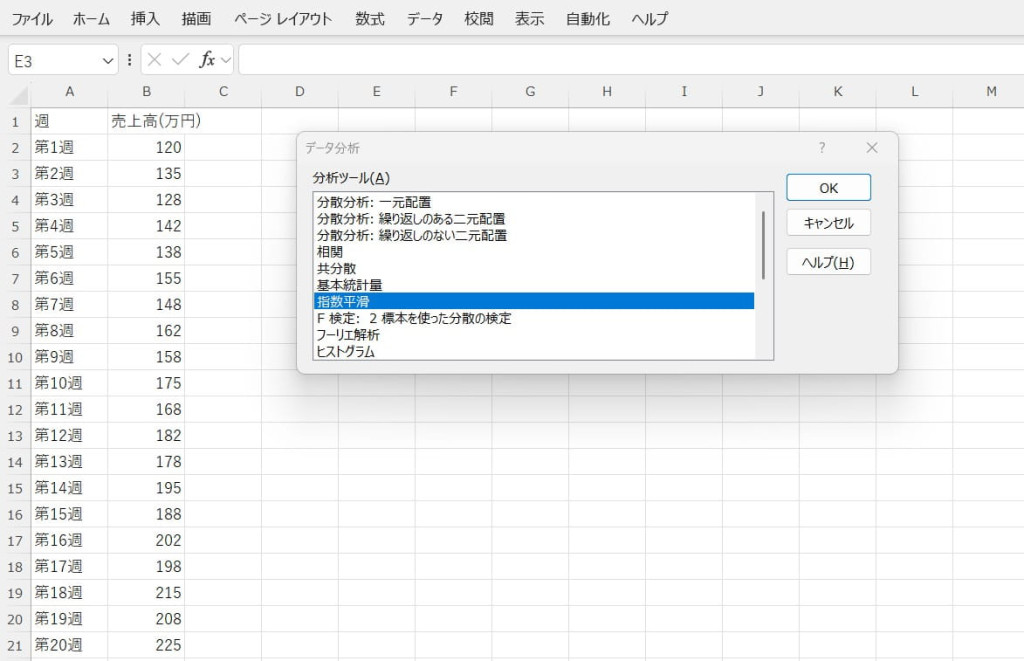
入力範囲や減衰率を設定します。減衰率とは、過去のデータの影響をどれだけ残すかを指定するための数値で、1に近いほど過去の影響が残りやすくなります。一般的には0.7程度、直近の変化を強く反映させたい場合は0.3程度が適切です。

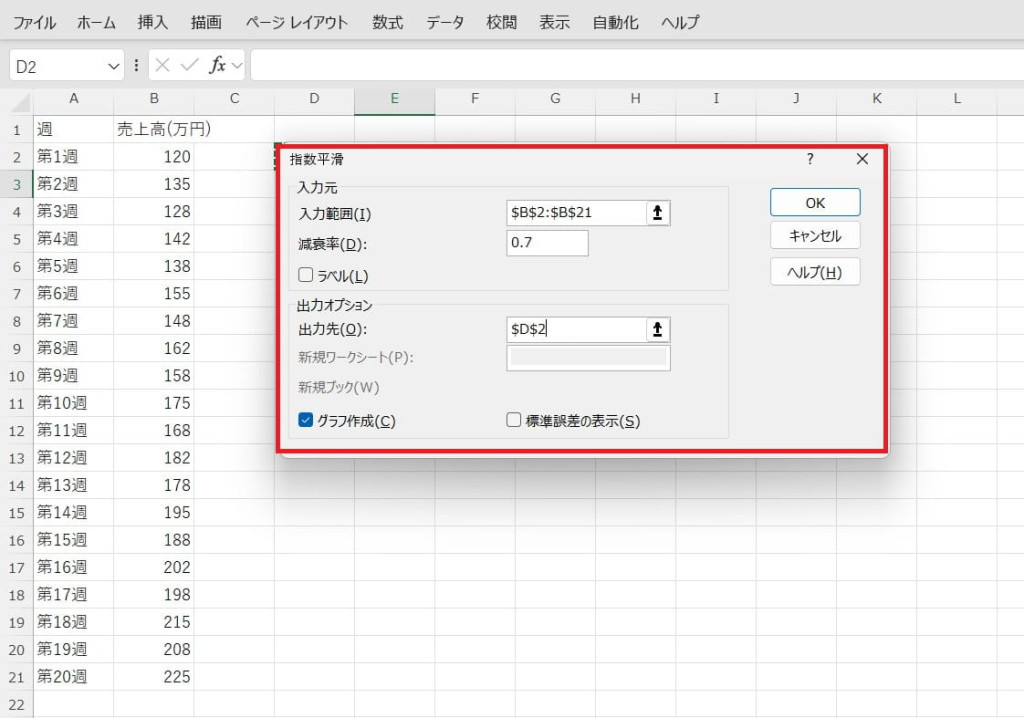
平滑化された結果を確認して予測に活用します。

フーリエ解析

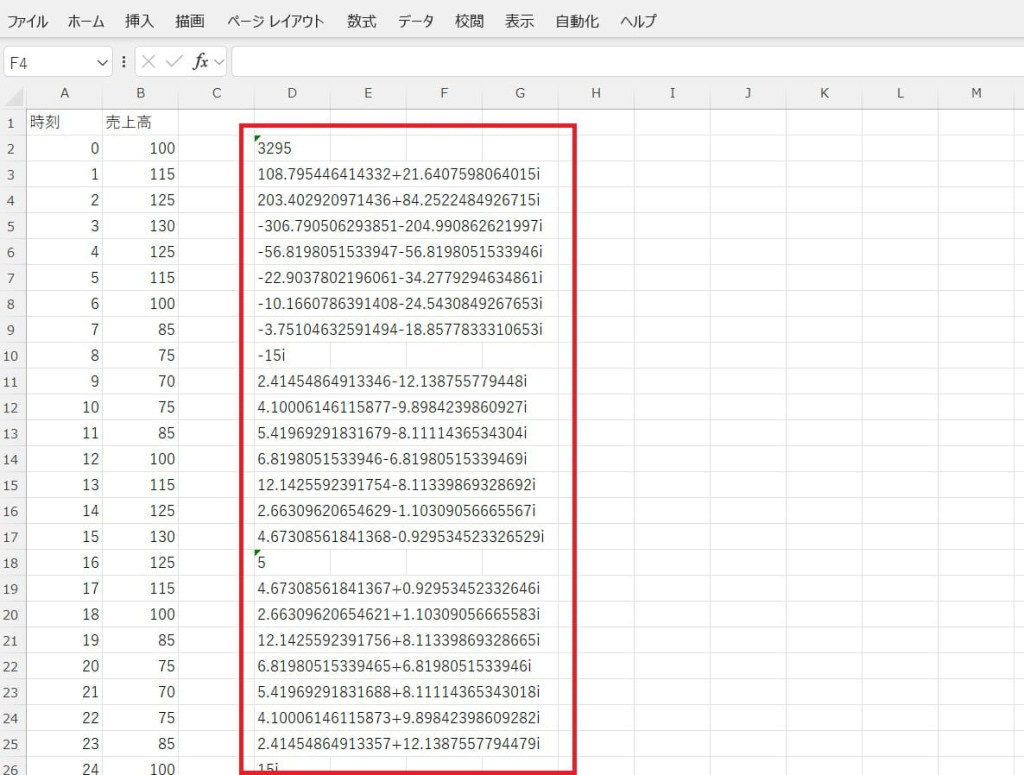
時系列データを周波数成分に分解する機能です。データに含まれる周期的なパターンやノイズの特性を解析し、視覚的に理解できます。フーリエ解析は、信号処理や音響解析に応用される分析手法です。

【フーリエ解析の使い方】

時系列データを列形式で入力します。

「データ分析」ツールでフーリエ解析を選択します。

入力範囲などを設定し、結果を出力します。

周波数成分を確認してデータの周期性を評価します。

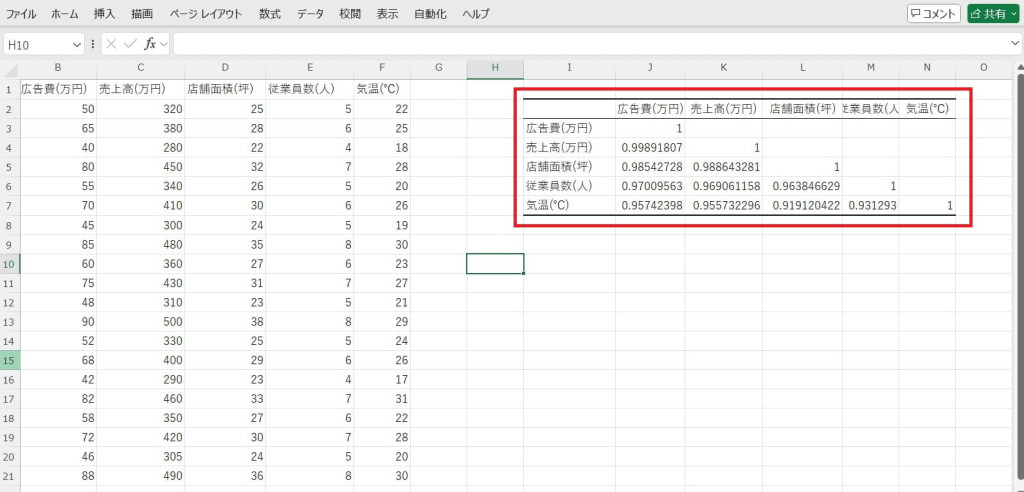
相関

2つの変数間の関係性を分析できます。相関係数が関係の強さと方向性を表し、一方が増えると他方も増える正の相関、一方が増えると片方が減る負の相関、お互いに関係がない無相関の識別が可能です。経済データや科学実験の解析などに応用されます。

【相関の使い方】

データを列形式で入力します。

「データ分析」から相関分析を実行します。

入力範囲や出力先を設定します。

相関係数が計算され、各要素同士の関係性を評価できます。

共分散

2つの変数間の変動を評価し、データの傾向や関係性を確認できる機能です。データの分布を比較して解析することができ、相関分析の補助として使用されます。

【共分散の使い方】

データを列形式で準備します。

「データ分析」ツールで共分散を選択します。

入力範囲を設定し、結果を出力します。

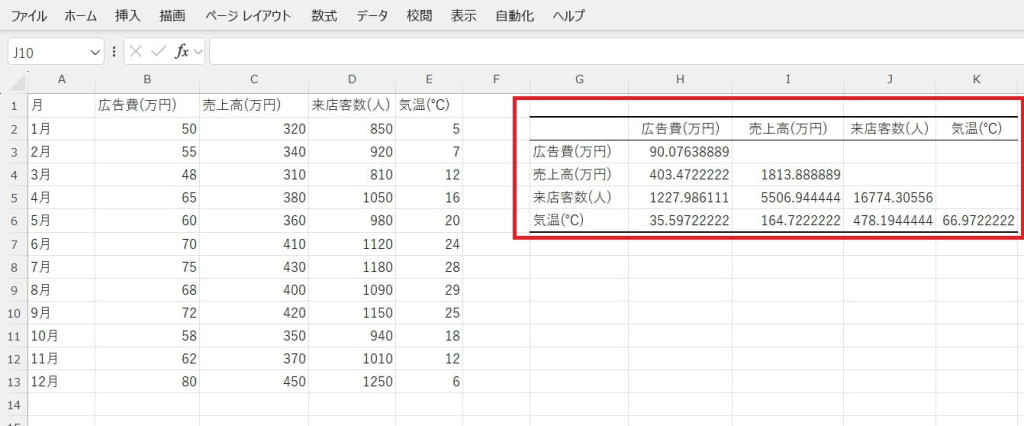
共分散値を確認して変数間の関係を評価します。値が大きくなっている要素ほど、相関関係の強い要素です。

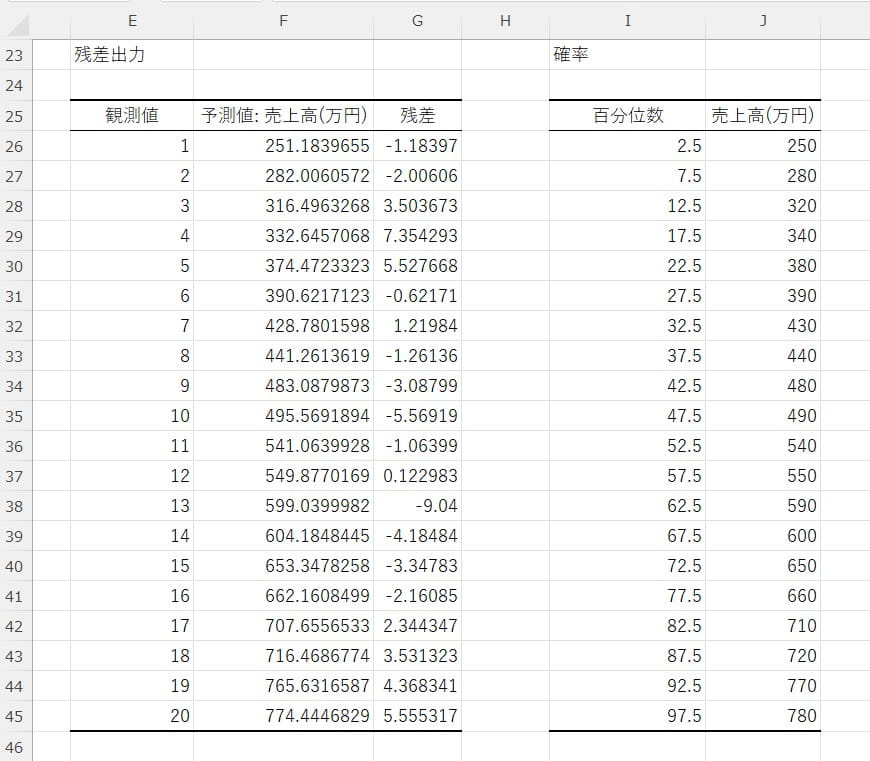
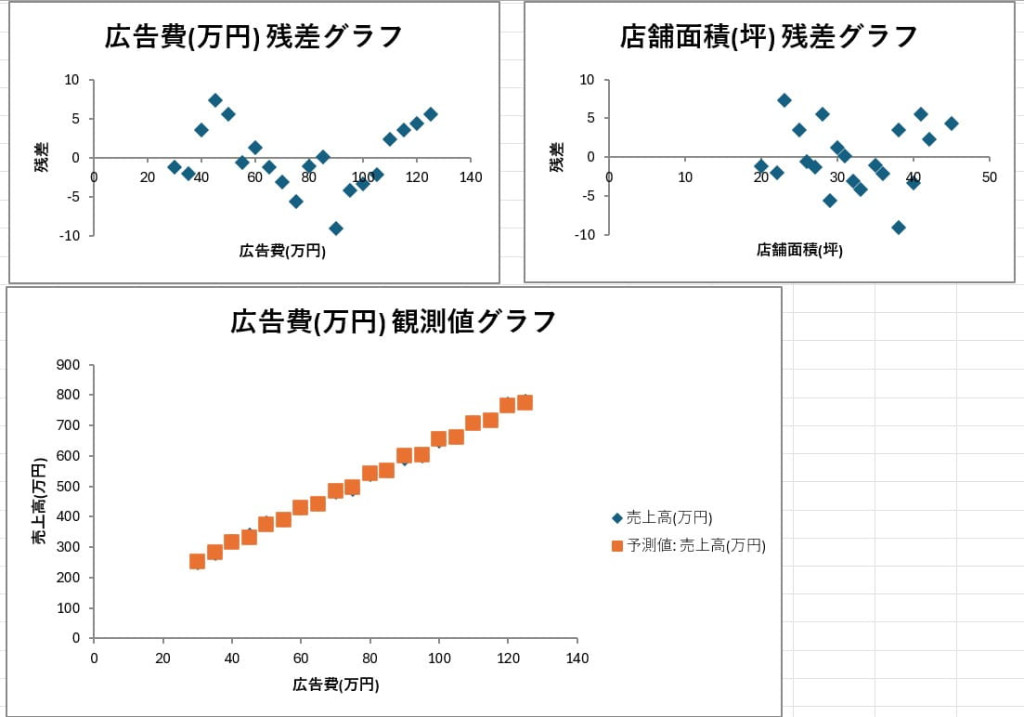
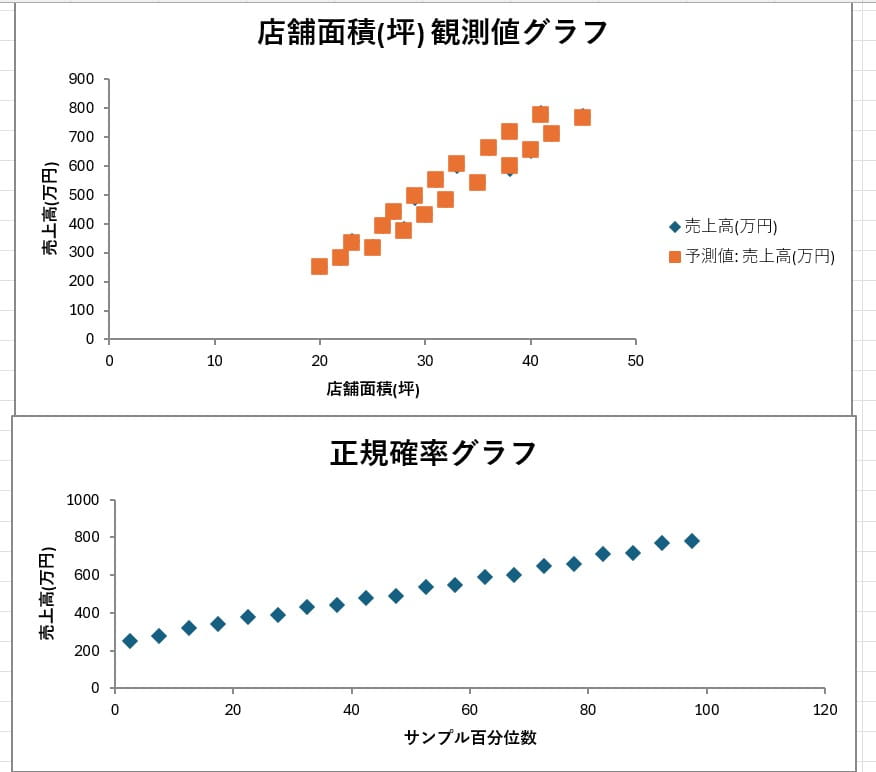
回帰分析

変数間の関係性をモデル化する機能です。独立変数を使って従属変数を予測したり、線形回帰や多項式回帰といった計算を実行したりできます。売上予測や市場分析への応用が可能です。

【回帰分析の使い方】

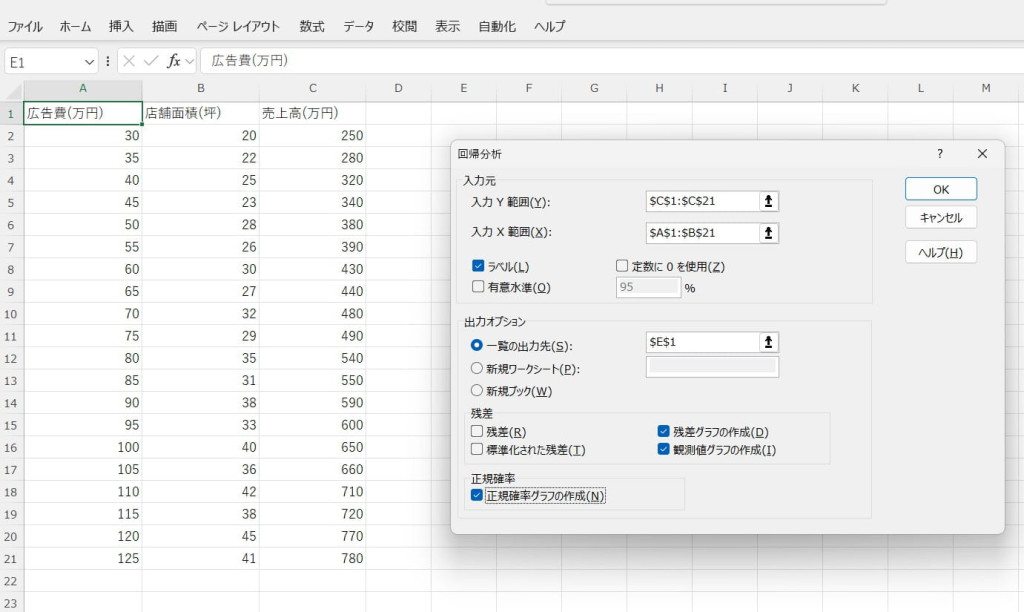
データを独立変数と従属変数に分けて入力します。今回は独立変数に広告費と店舗面積、従属変数に売上高を割りあてています。

分析ツールの一覧から「回帰分析」を選択します。

入力範囲や出力オプションを設定します。

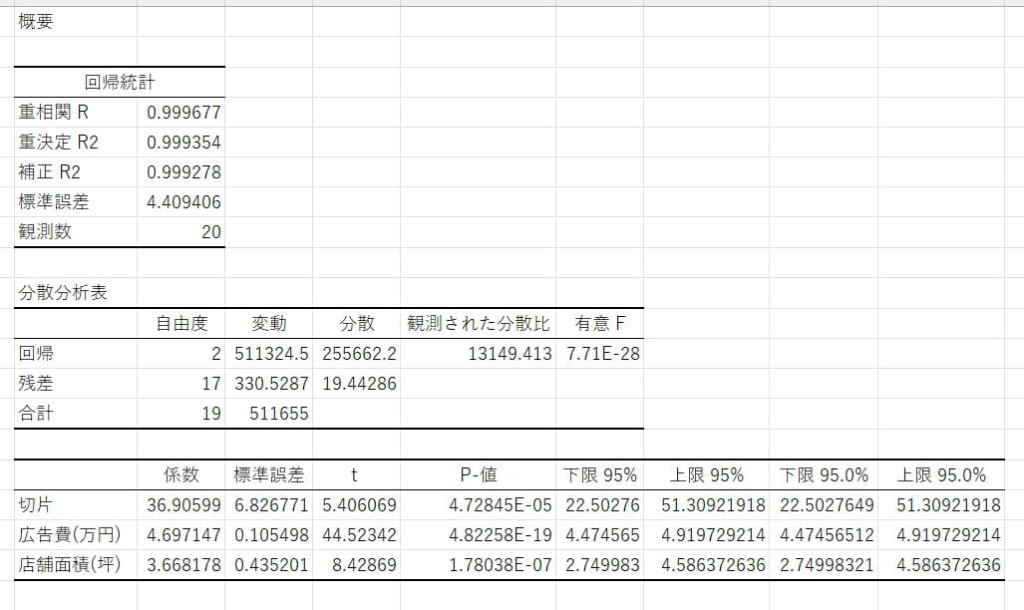
回帰分析の結果を確認し、係数や統計量を評価します。

t検定（一対の標本による平均の検定）

同一グループの前後比較など、2つの関連する標本の平均値の差を検定する機能です。統計的に有意な差があるかを確認し、処置効果や時間による変化を評価できます。例えば、実験結果やマーケティングキャンペーンの効果測定への応用が可能です。

【t検定（一対の標本による平均の検定）の使い方】

対応する2組のデータを入力します。

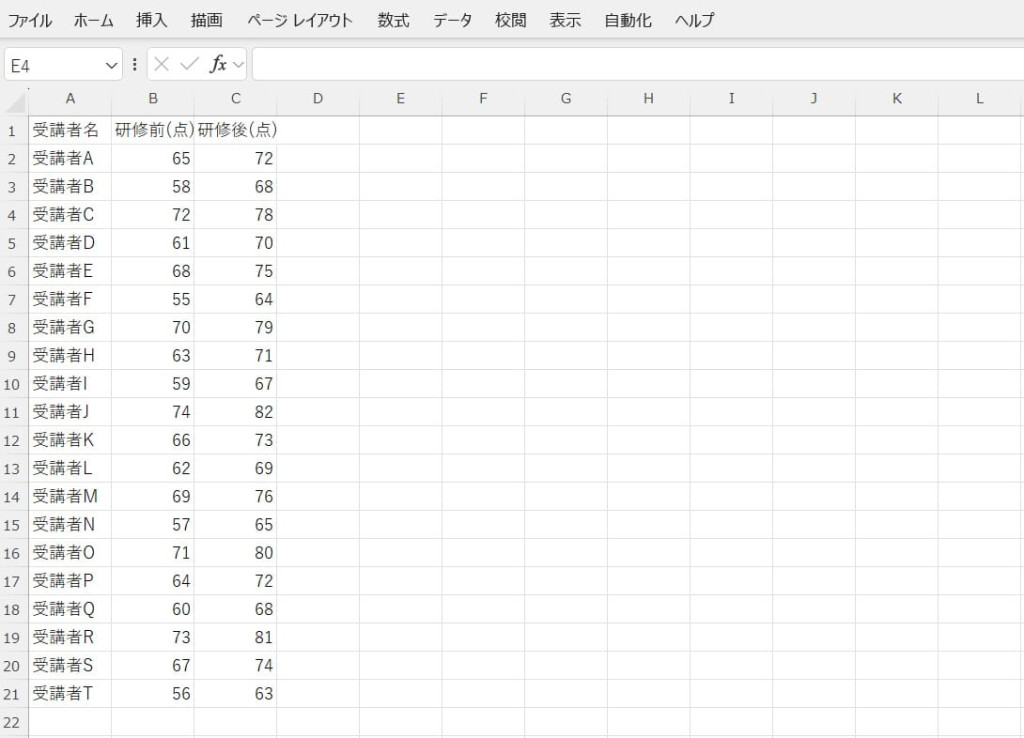
データ分析ツールで「t検定（一対の標本による平均の検定）」を選択します。

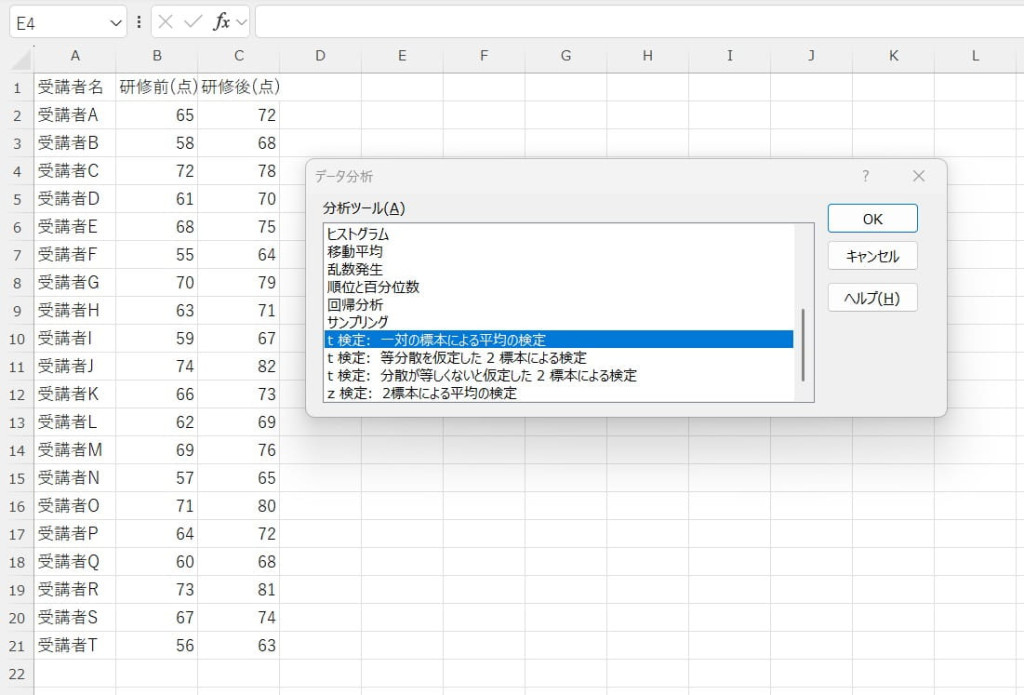
入力範囲などを設定し、結果を出力します。

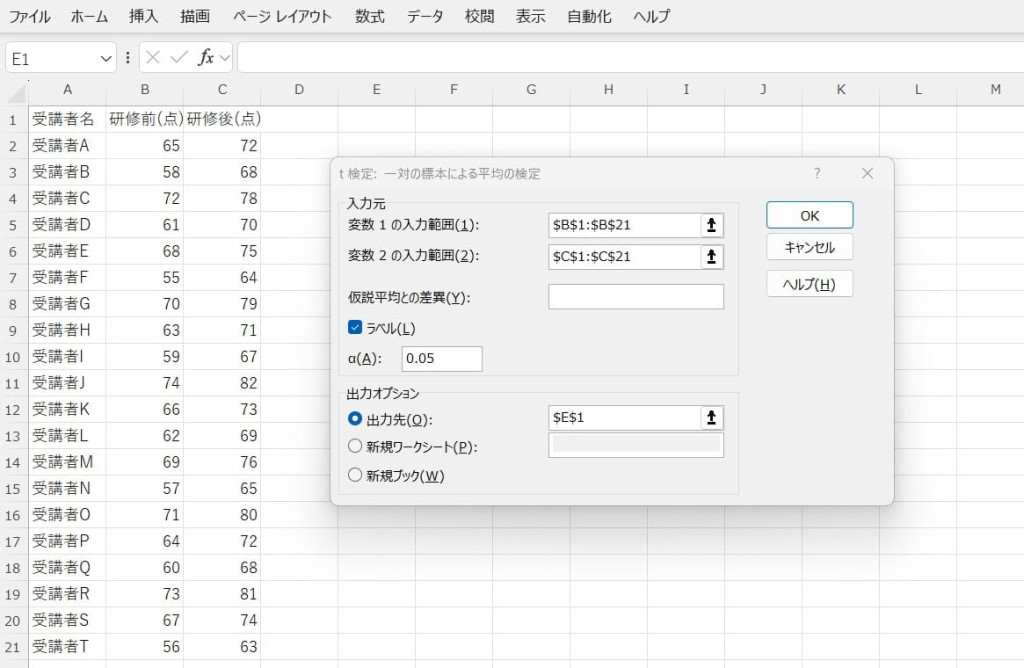
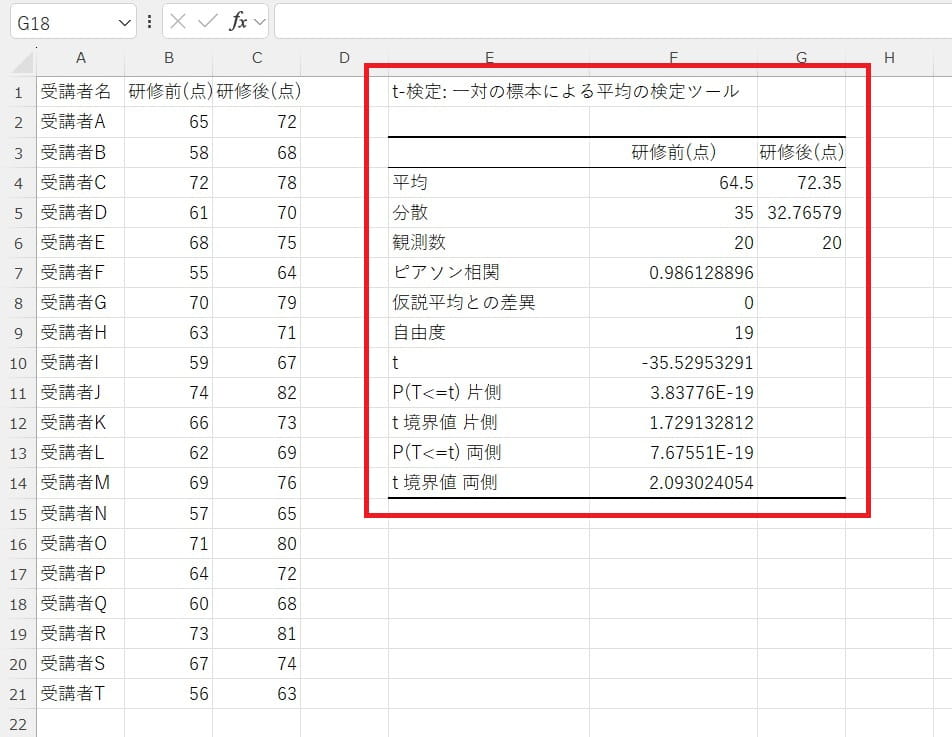
t値やp値を確認して有意性を判断します。今回の場合、t値の絶対値（35.53）が非常に大きいため、研修前後の平均点の差は偶然ではなく、明確な差があると判断できます。また、p値がほとんど0に近い値であり、0.05（5%）を大きく下回っているため、研修前後の得点の差は統計的に有意です。

t検定（等分散を仮定した2標本による検定）

2つの独立した標本の平均値の差を検定する機能です。標本間で分散が等しいと仮定して解析を行い、グループ間の平均値の差が統計的に有意かを評価できます。製品の性能や市場調査の結果などを比較する際に活用されます。

【t検定（等分散を仮定した2標本による検定）の使い方】

2つの独立した標本データを入力します。

データ分析ツールで「t検定（等分散を仮定した2標本による検定）」を選択します。

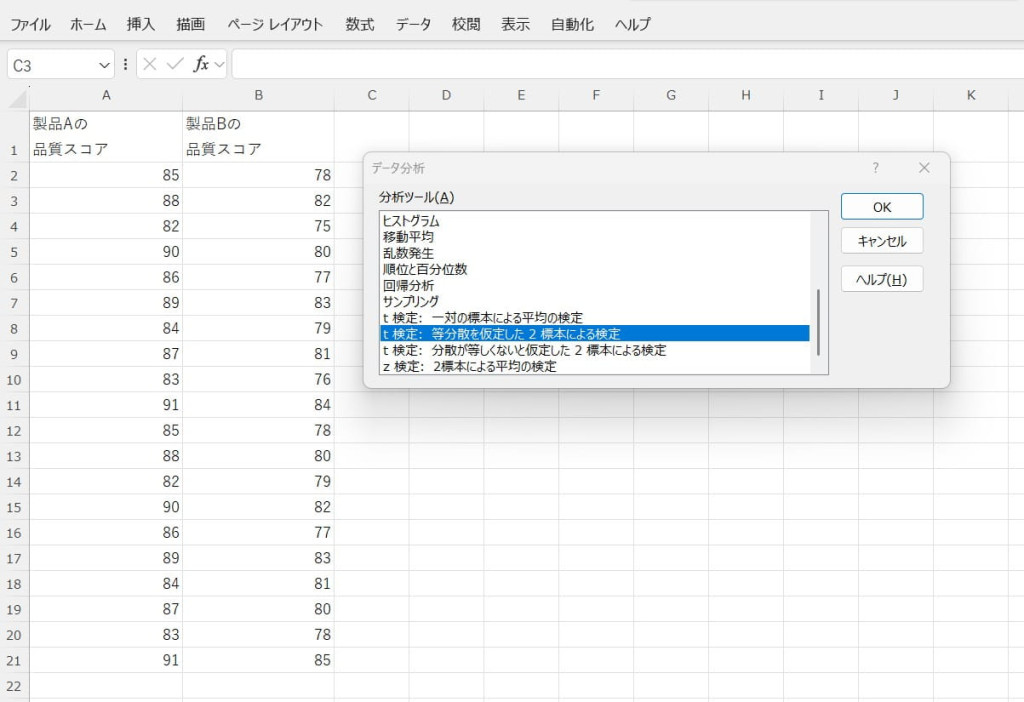
入力範囲などを設定し、結果を出力します。

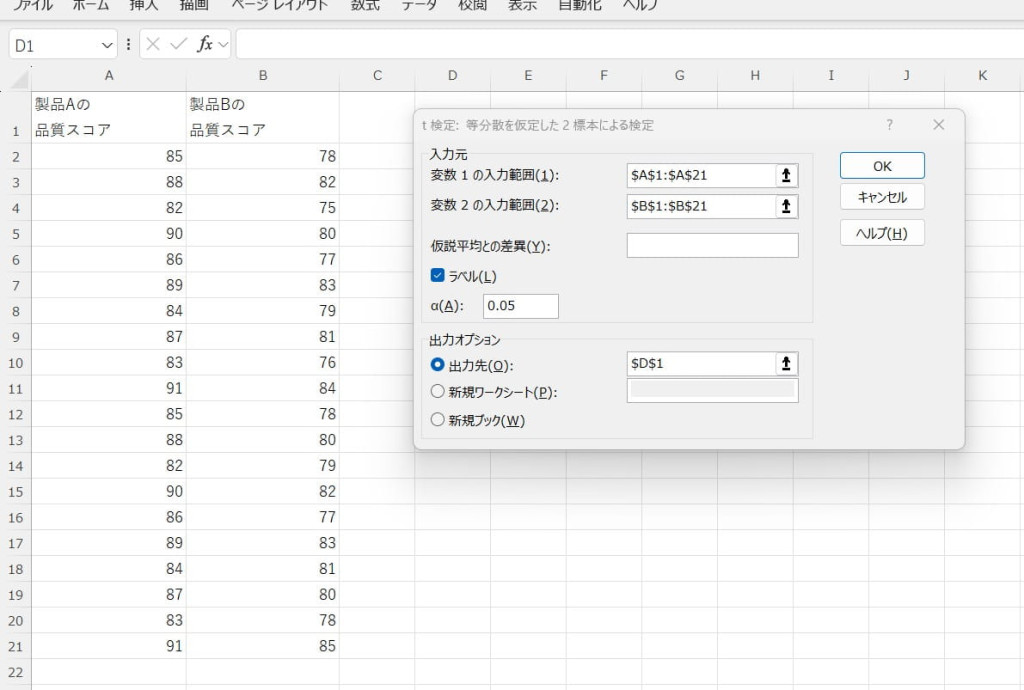
t値やp値を確認して平均値の差を評価します。t値が約7.35であり、t境界値2.024を大きく上回るため、製品Aと製品Bの平均スコアには明確な差があると判断できます。また、p値が0.05を下回っているため、2つの製品の品質スコアの差は統計的に有意です。

t検定（分散が等しくないと仮定した2標本による検定）

2つの独立した標本の平均値の差を検定する機能です。標本間の分散が等しくない場合でも、適切な解析を行い、標本間の平均値の差が統計的に有意かを評価できます。実験条件や異なるグループ間の比較に応用可能です。

【t検定（分散が等しくないと仮定した2標本による検定）の使い方】

2つの独立した標本データを入力します。

データ分析ツールで「t検定（分散が等しくないと仮定した2標本による検定）」を選択します。

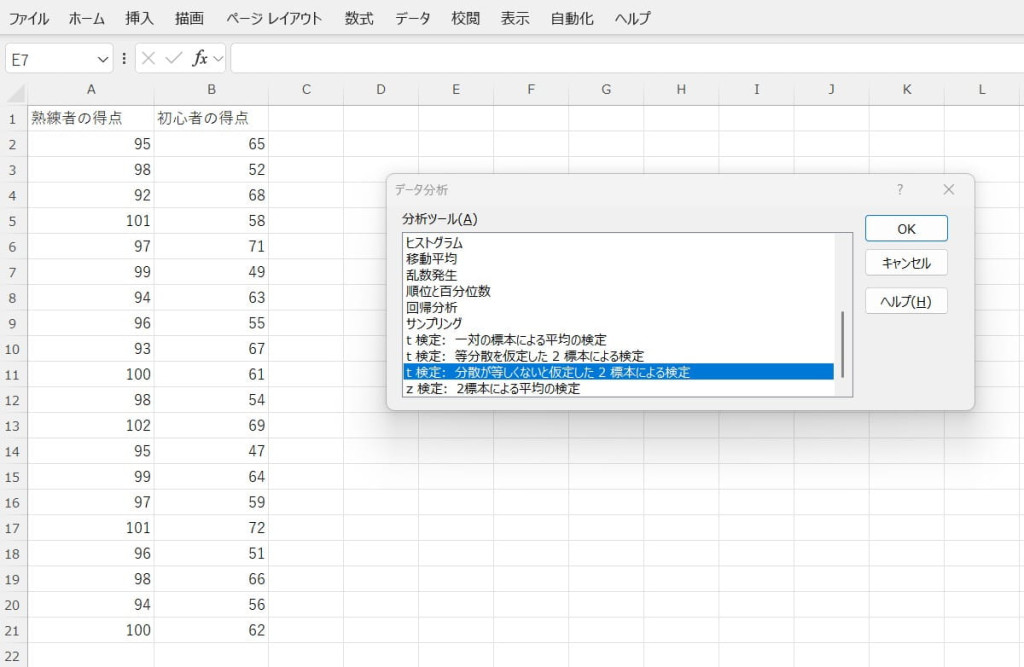
入力範囲などを設定し、結果を出力します。

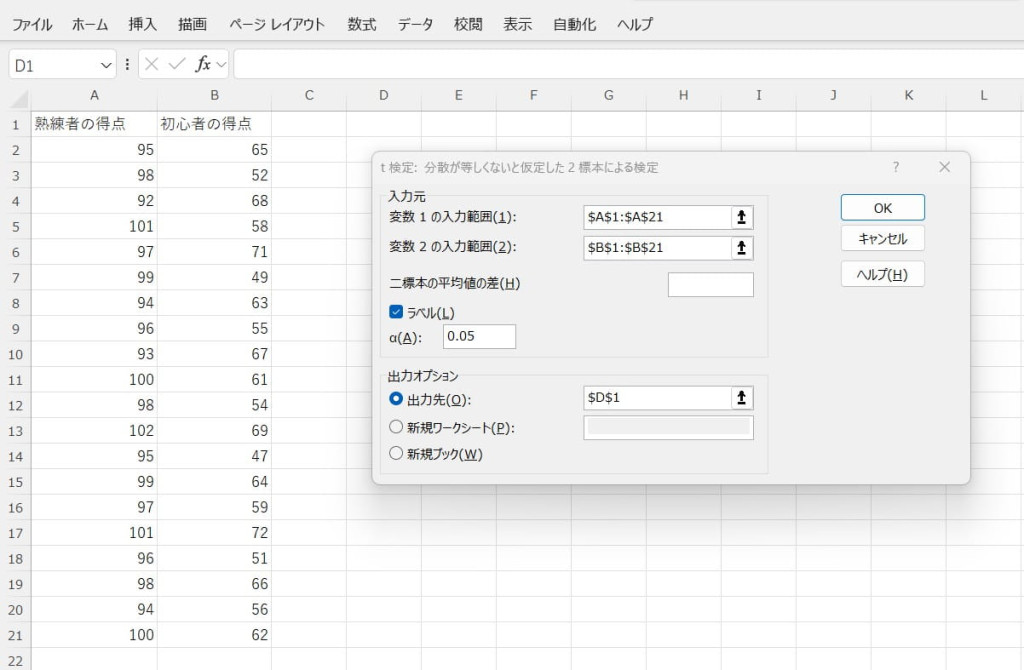
t値やp値を確認して平均値の差を評価します。今回のデータでは、熟練者の得点と初心者の得点の分散（ばらつきの度合い）が約8と約56で大きく異なっています。t値が約20.57と、t境界値の約2.064を大きく上回っているため、熟練者と初心者の平均点には明確な差があると判断できます。また、p値がほとんど0に近い値のため、統計的に有意です。

z検定（2標本による平均の検定）

2つの独立した標本の平均値の差を検定する機能です。標本サイズが大きく、標準偏差が既知の場合に使用できます。大規模な調査結果や実験結果などの比較が可能です。

【z検定（2標本による平均の検定）の使い方】

比較対象となる２つのデータを入力します。

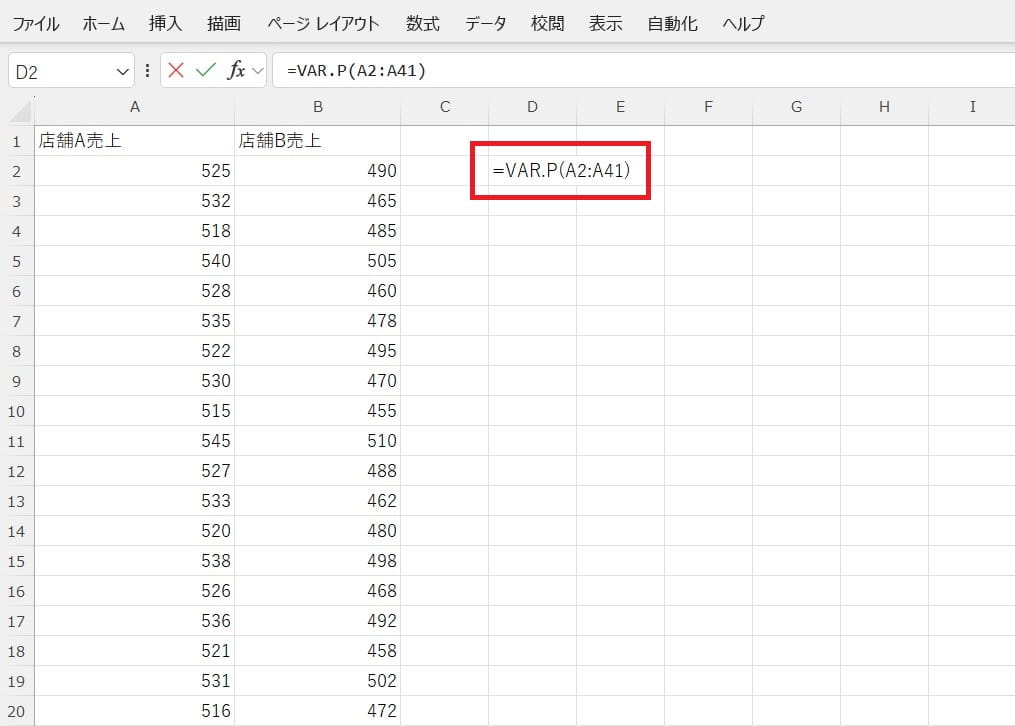
z検定ではそれぞれのデータの分散を入力する必要があるため、「VAR.P関数」を使ってあらかじめ算出しておきます。

データ分析ツールで「z検定（2標本による平均の検定）」を選択します。

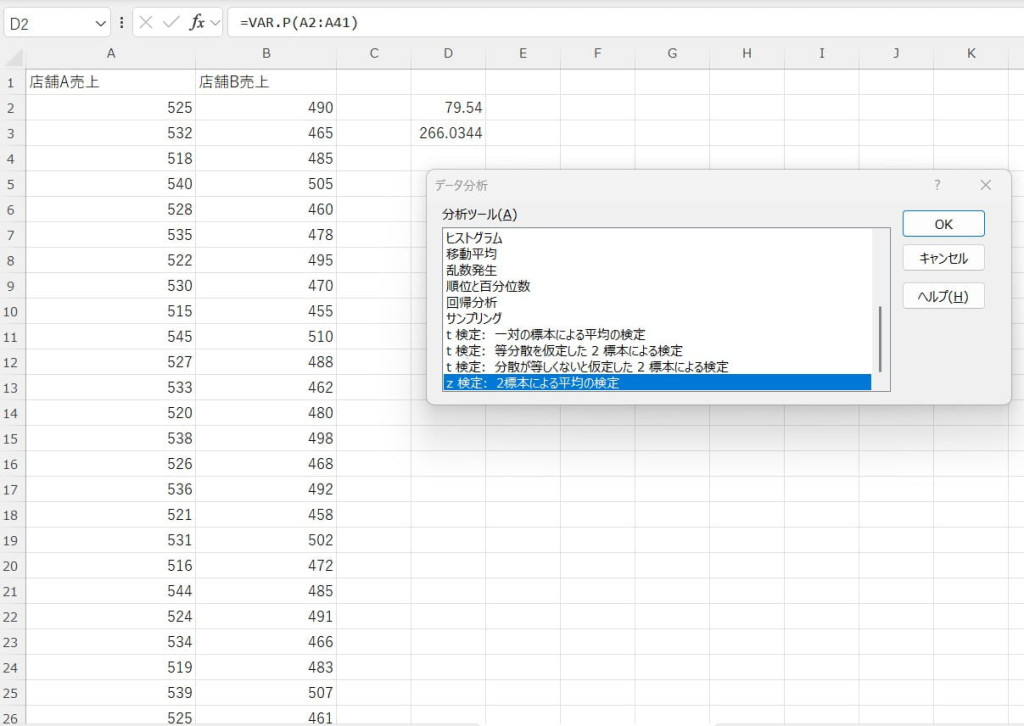
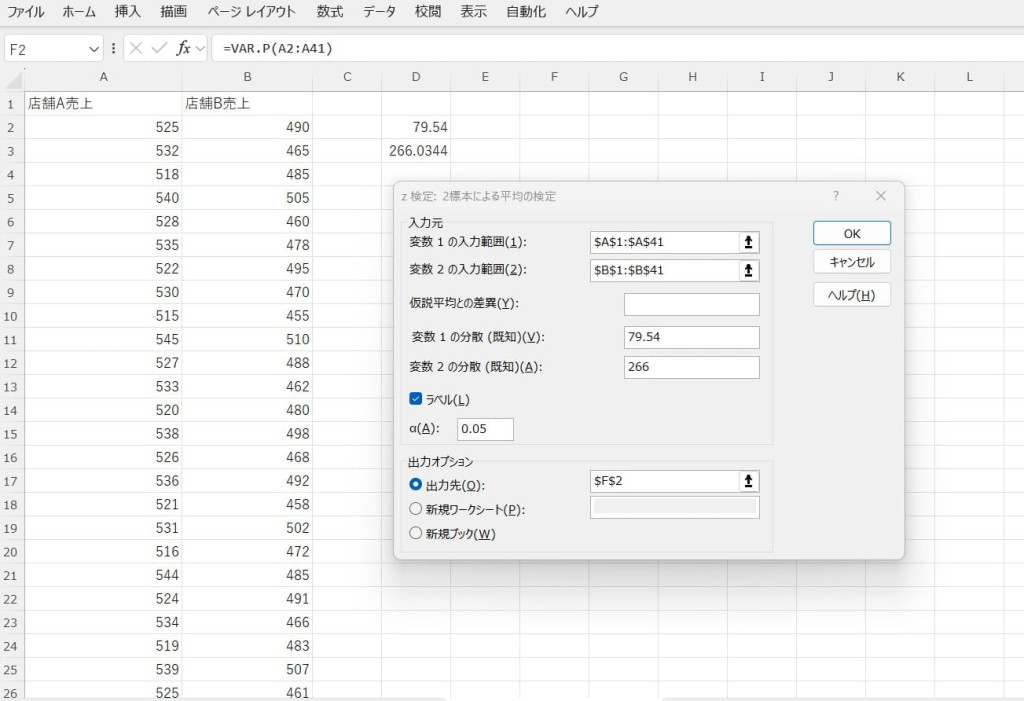
入力範囲や分散などを設定し、結果を出力します。

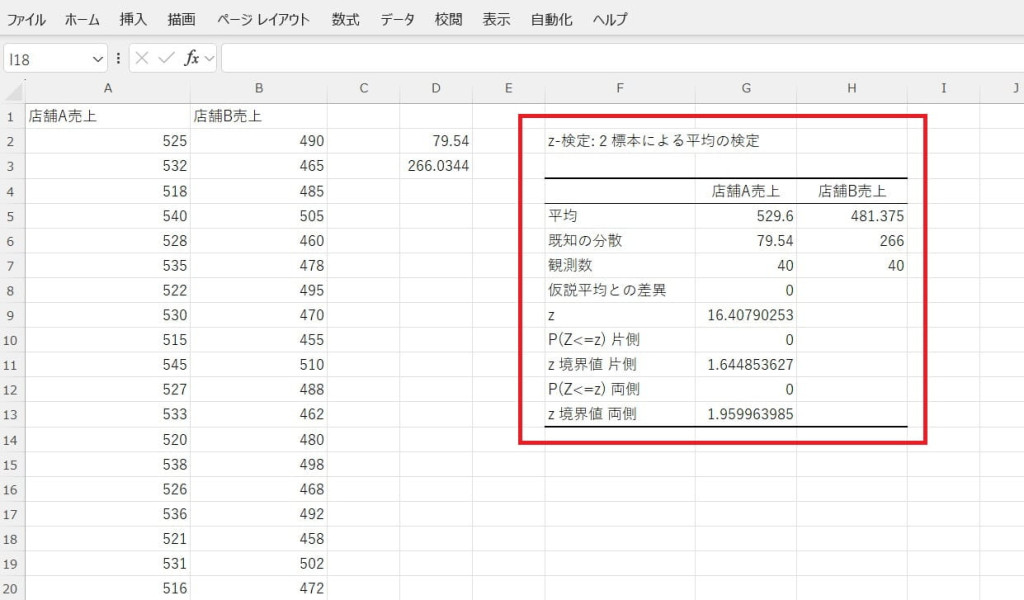
z値やp値を確認して平均値の差を評価します。今回のデータの場合、z値が16.41とz境界値の約1.96を大幅に上回る値のため、店舗Aと店舗Bの平均売上には大きな差があると評価できます。また、p値が0のため、この差は統計的に有意です。

F検定（2標本を使った分散の検定）

2つのデータセットの分散が等しいかを計算し、グループ間のばらつきの違いを評価できる機能です。t検定などの前提条件を確認するために使用されます。実験結果の分析や品質管理に応用可能です。

【F検定（2標本を使った分散の検定）の使い方】

2つのデータセットを入力します。

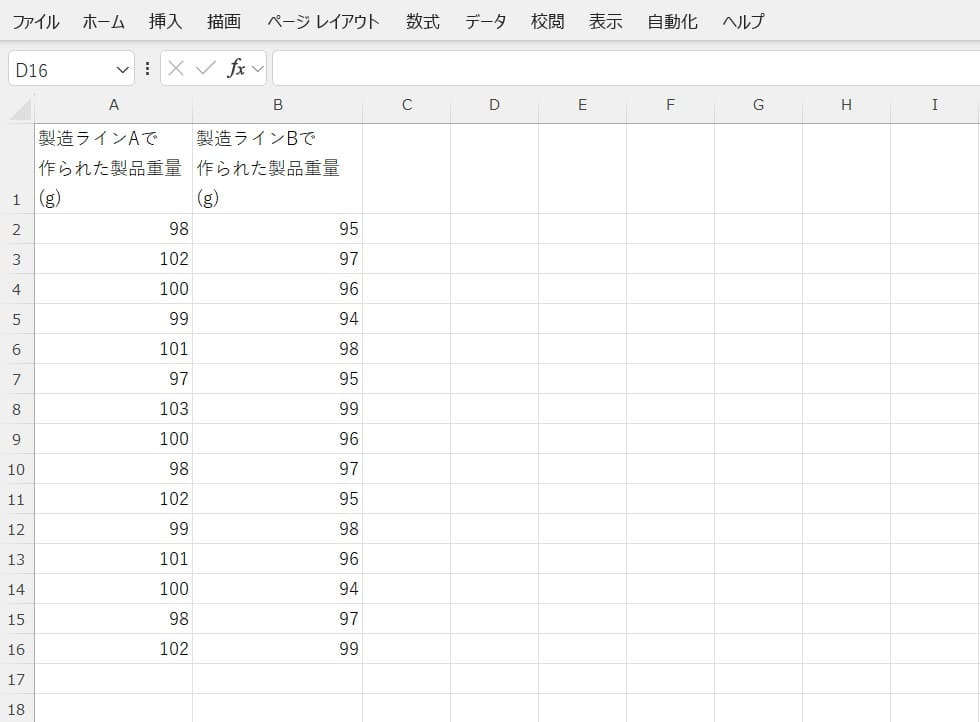
「データ分析」メニュー内のF検定機能を利用します。

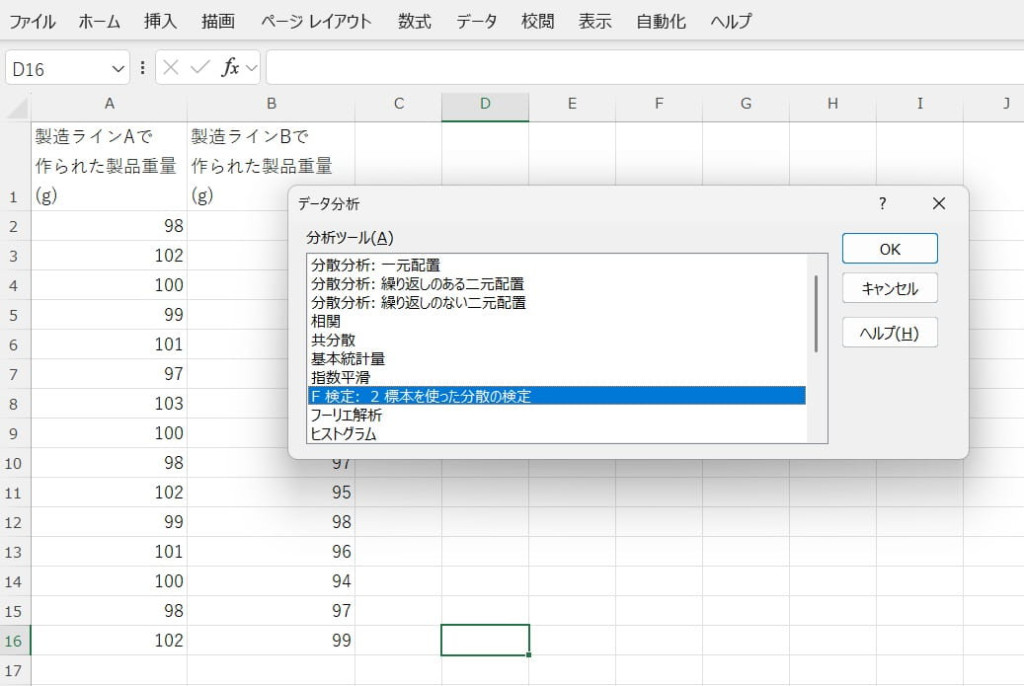
入力範囲を指定し、結果を出力します。

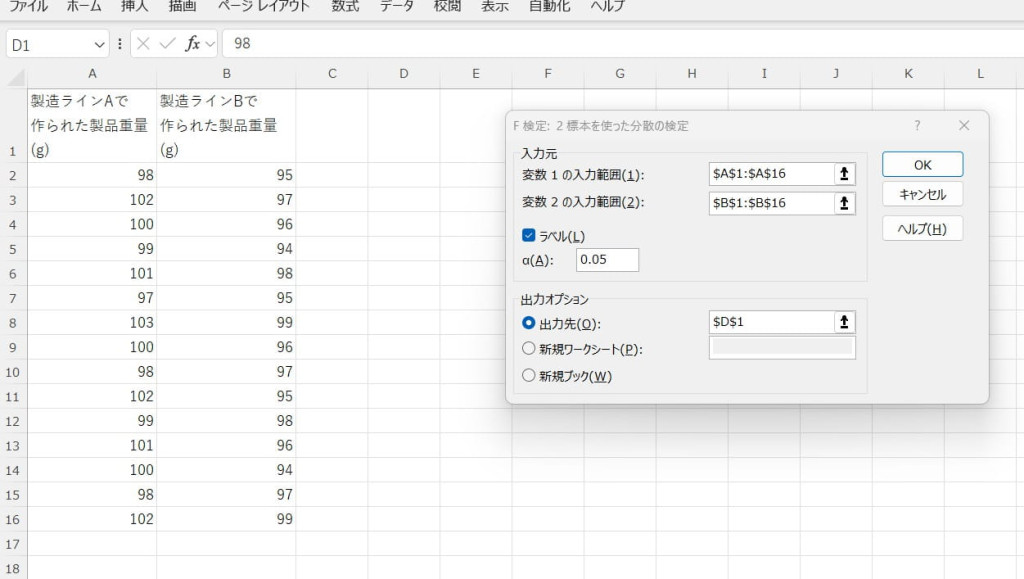
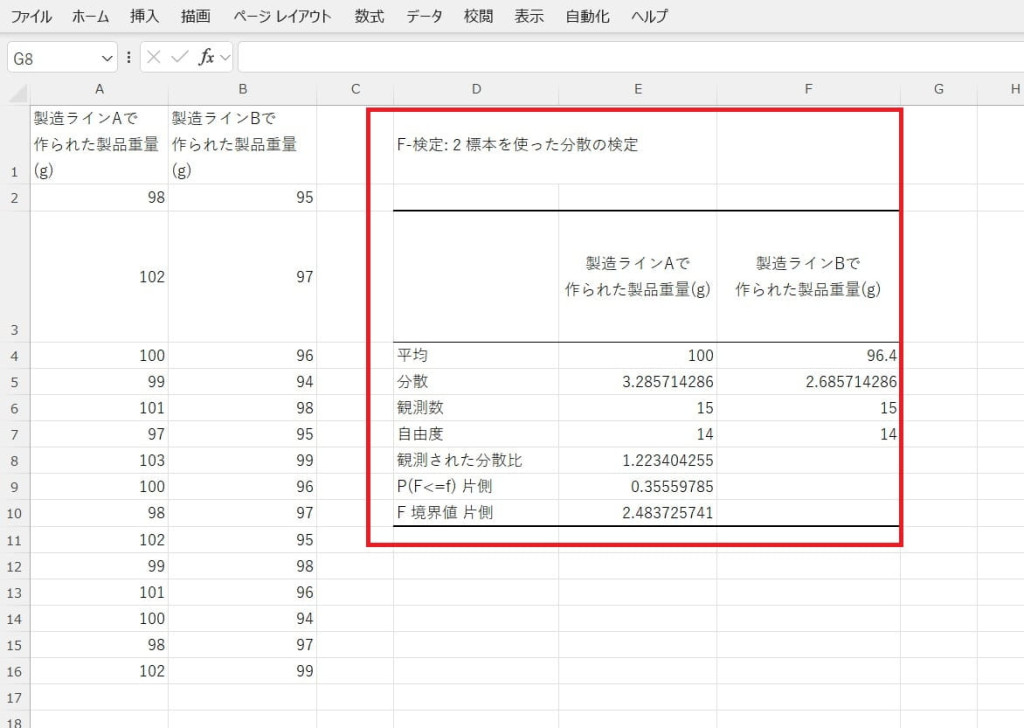
P値やF値を確認して分散の差を評価します。

分散分析（繰り返しのある二元配置）

2つの要因が結果に与える影響を、繰り返しの測定を考慮して分析できる機能です。

例えば、授業の方法（オンラインか対面か）と、授業の時間帯（午前か午後か）という2つの要因が、テストの点数という結果にどう影響を与えているかなどを分析できます。この例の場合、繰り返しのある二元配置とは、同じ生徒がオンライン授業と対面授業の両方を受けて、それぞれに対するテスト結果がデータに含まれているケースなどを表します。

【分散分析（繰り返しのある二元配置）の使い方】

データを行列形式で入力します。

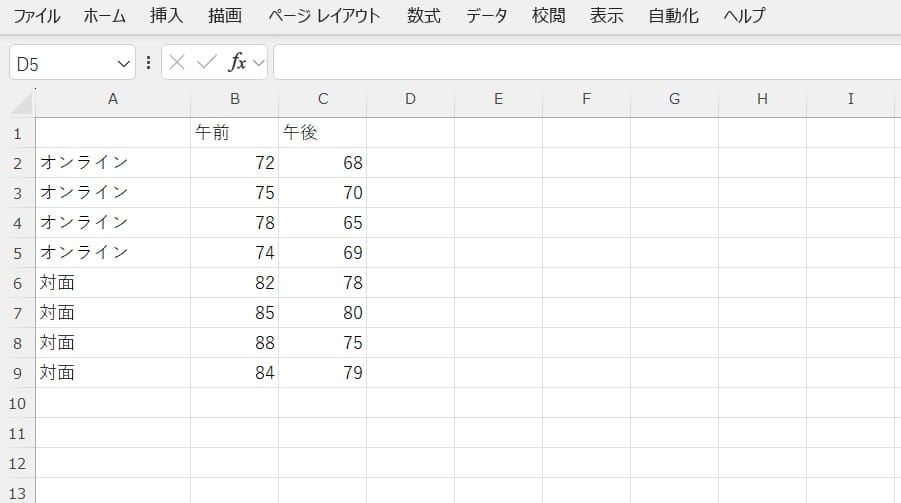
データ分析機能の「分散分析」（二元配置）を選択します。

今回は、1標本あたり4回繰り返していると仮定して作ったデータを分析するため、「1標本あたりの行数」は4に設定します。

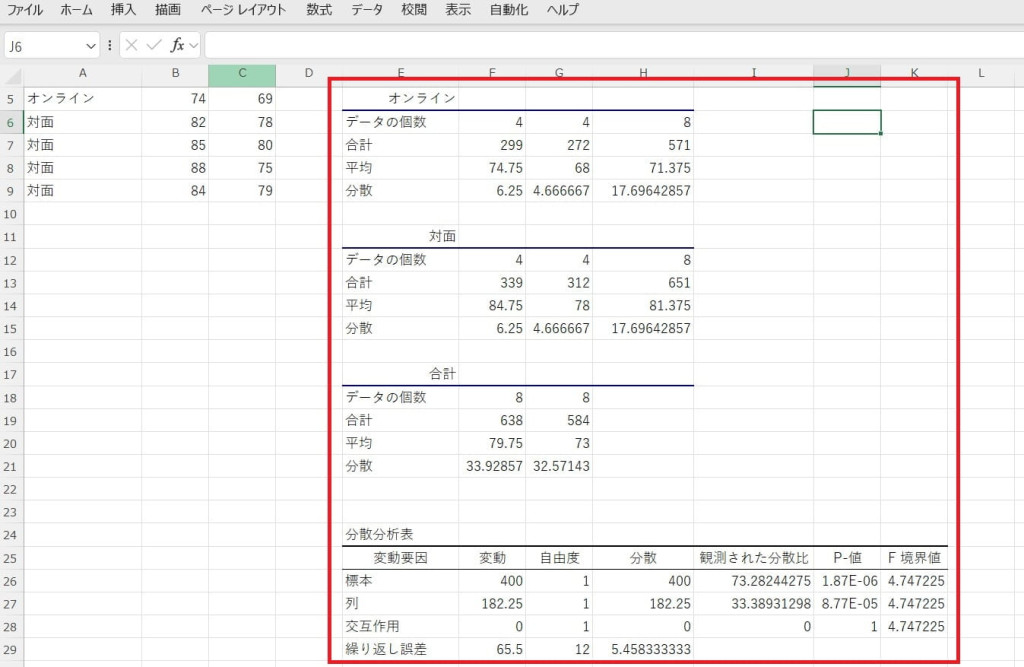
結果を確認し、要因間の相互作用を評価します。

分散分析（繰り返しのない二元配置）

2つの要因が結果に与える影響を、繰り返し測定を考慮せずに分析できる機能です。

例えば、授業の方法（オンラインか対面か）と、授業の時間帯（午前か午後か）という2つの要因が、テストの点数にどう影響を与えているかなどを分析できます。繰り返しのない二元配置とは、被験者を「オンライン・午前」「オンライン・午後」「対面・午前」「対面・午後」などの4つのグループに分け、同じ人が複数のパターンを繰り返さないようにするケースなどを表します。

【分散分析（繰り返しのない二元配置）の使い方】

データをExcelに入力します。

データタブ内の「データ分析」機能から、二元配置の分散分析を選びます。

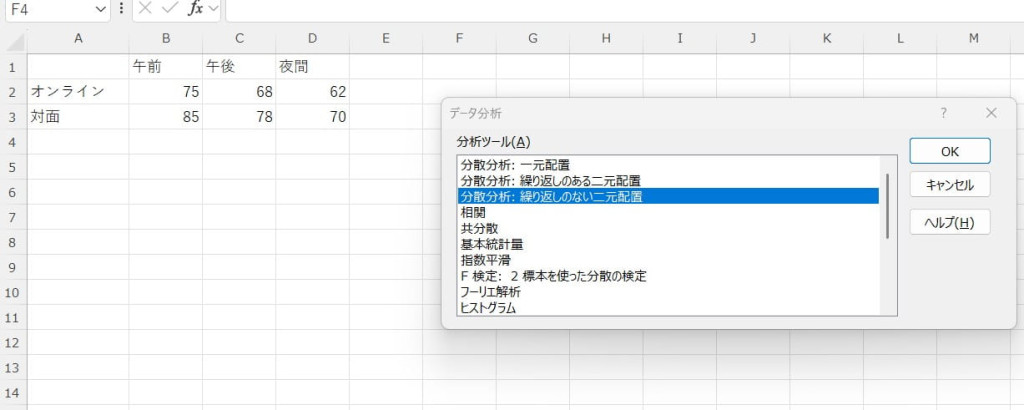
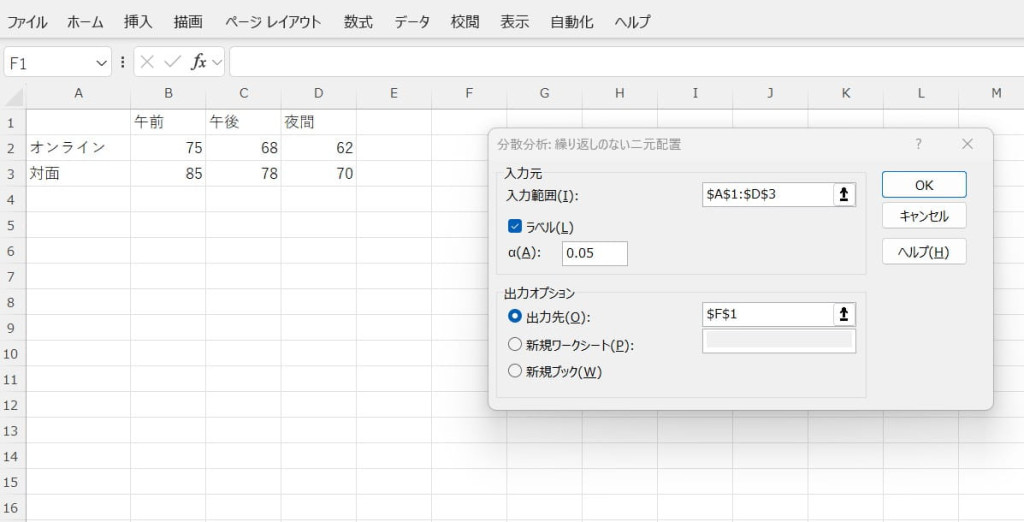
入力範囲や出力先を設定します。

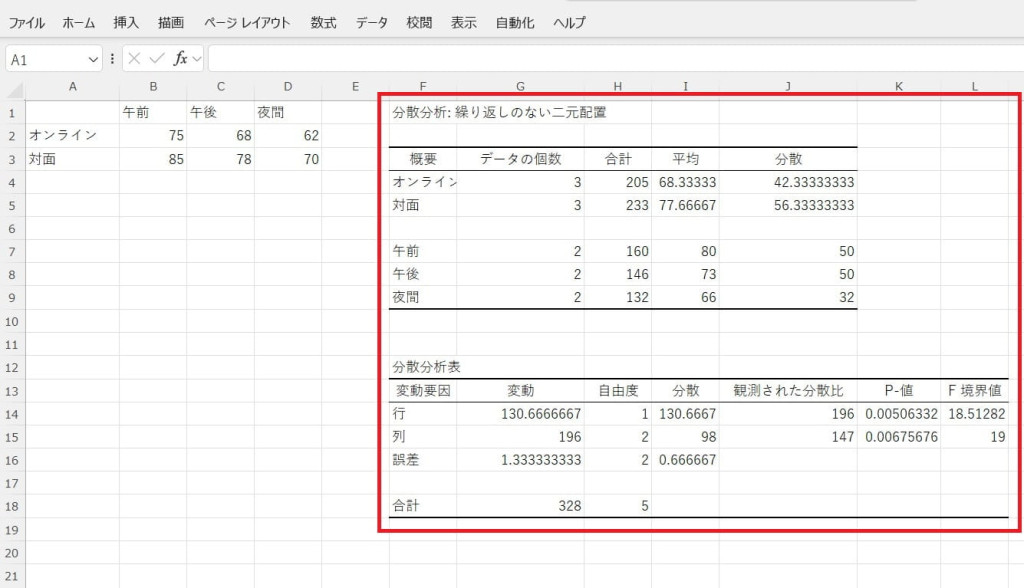
出力結果を確認し、P値やF値を評価します。

分散分析（一元配置）

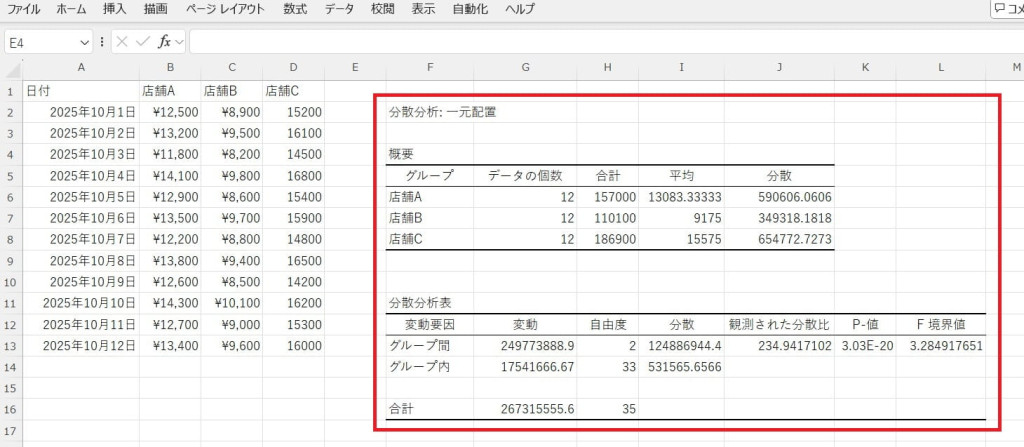
複数のグループ間で、平均値の差を検定する機能です。分散の割合を計算してデータのばらつきを評価することで、グループ間の差が統計的に有意かどうかを確認できます。実験結果の分析や製品の性能評価などに応用される機能です。

【分散分析（一元配置）の使い方】

データをExcelシートに入力し、グループごとに整理します。

「データ分析」から「分散分析：一元配置」を選択します。

入力範囲などを指定します。

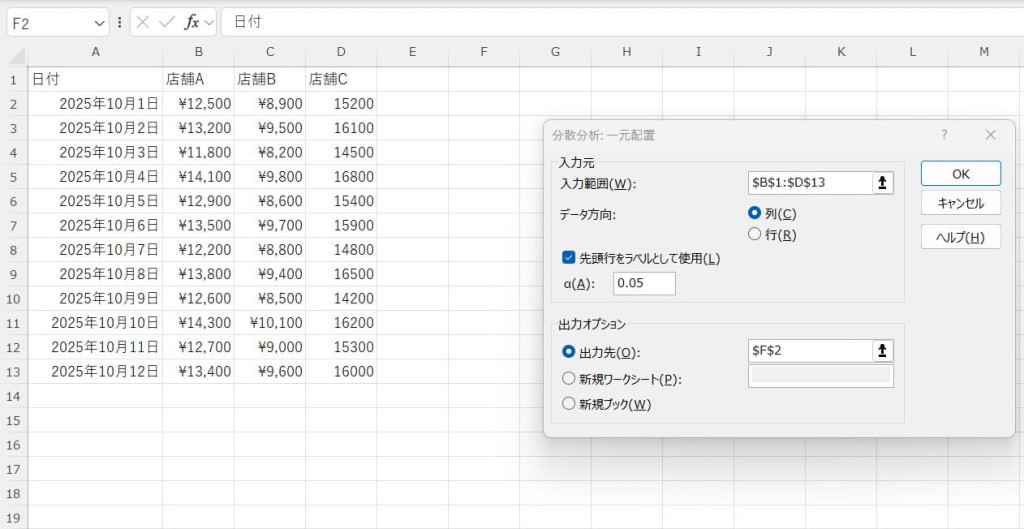
結果を確認し、F値やp値を評価します。

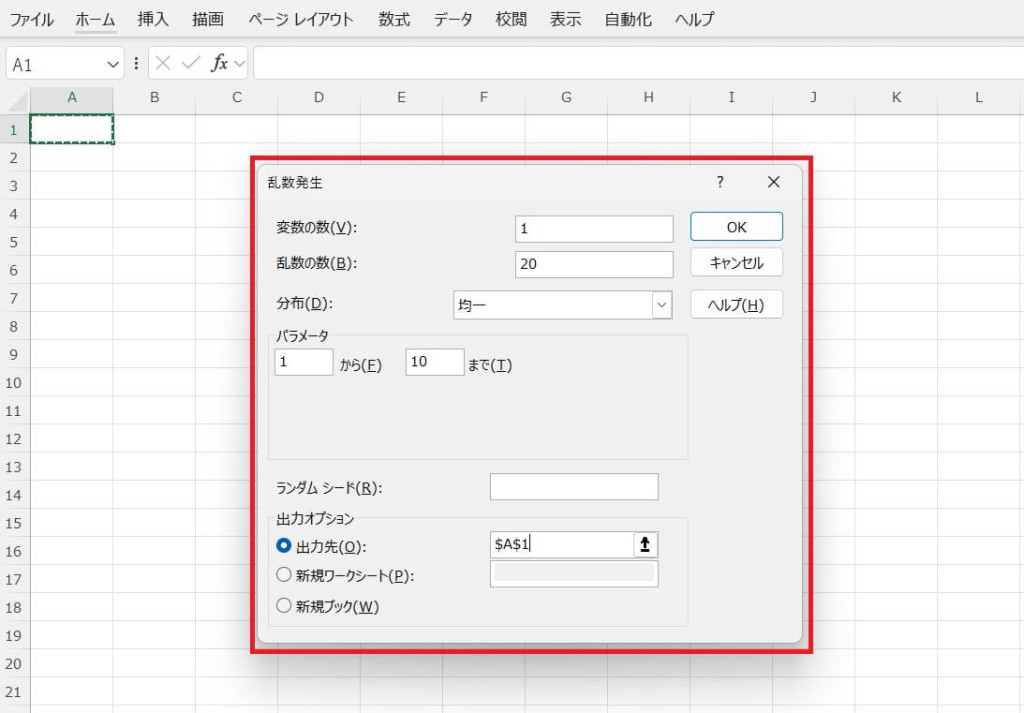
乱数発生

指定した範囲内でランダムな数値を生成する機能です。ランダムな数値を使ってシミュレーションを行うモンテカルロ法や統計的仮説検定、データを無作為に抽出したい場合などに活用されます。また、テストデータや仮想データの作成にも役立ちます。

【乱数発生の使い方】

「データ分析」ツールで乱数発生を選択します。

変数の数（列数）や乱数の数（個数）、ランダムな値を生成するための分布などを設定します。

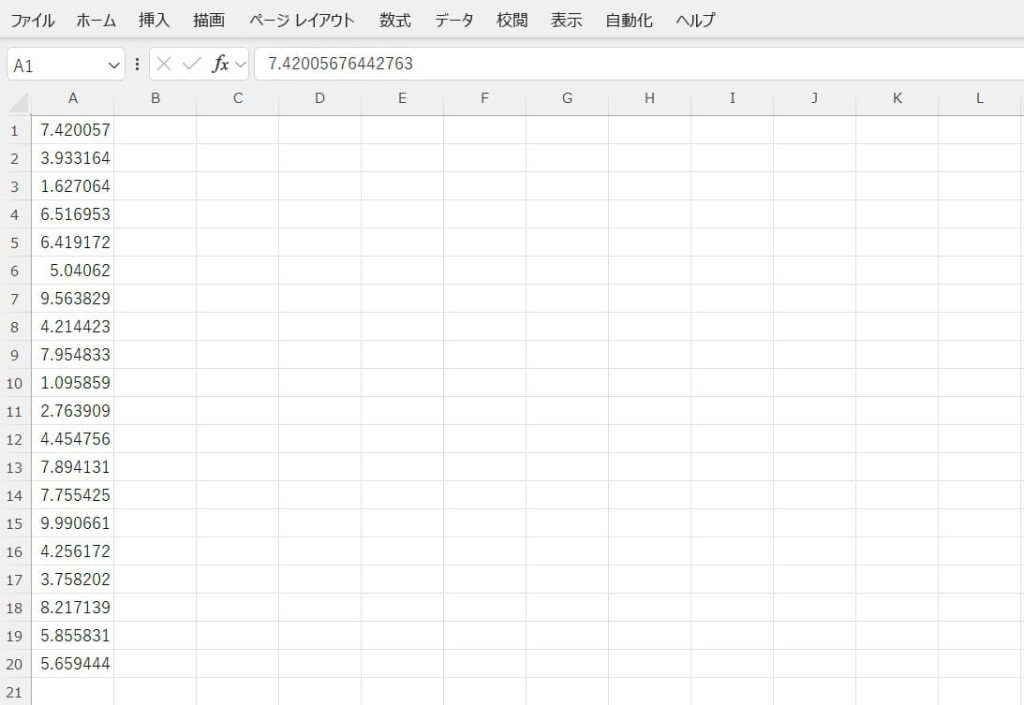
出力された乱数を確認して使用します。今回の例では、1～10までの範囲内でランダムな数値が20個生成されました。

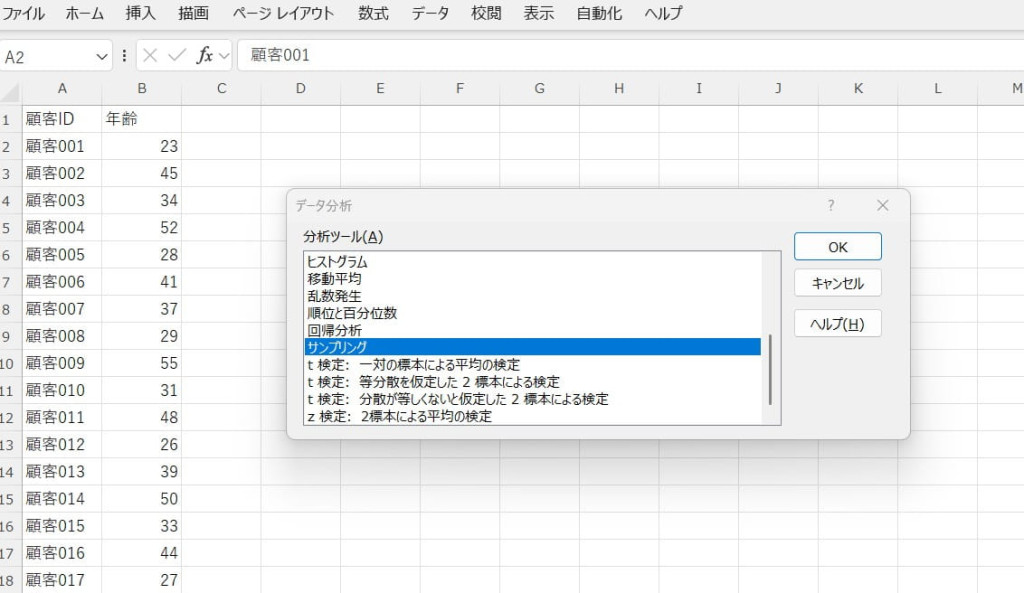
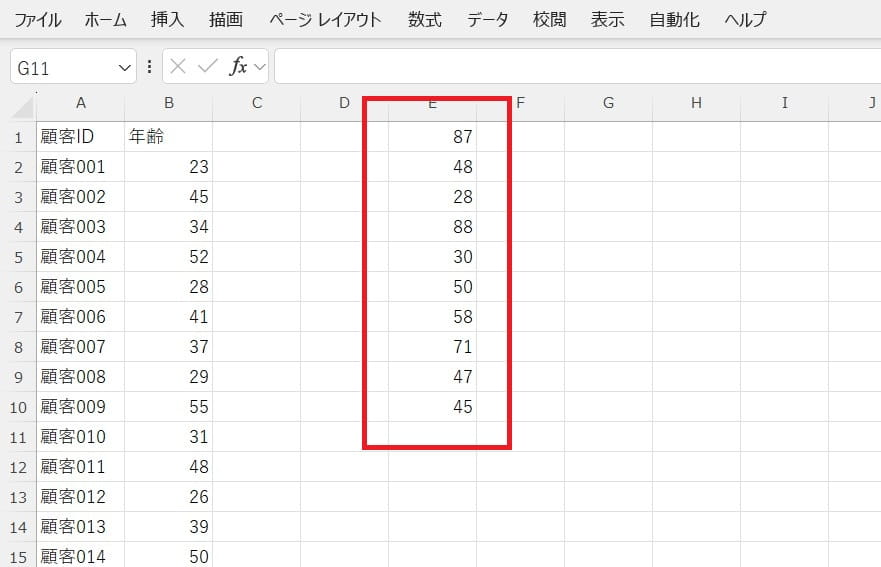
サンプリング

大量のデータからランダムにサンプルを抽出する機能です。サンプルデータを使った統計分析ができ、試験や調査結果を効率的に解析できます。モンテカルロ法やシミュレーションに応用可能です。

【サンプリングの使い方】

サンプリング対象となるデータを入力します。

データ分析ツールで「サンプリング」を選択します。

入力範囲や標本の採取方法、抽出するデータの個数などを設定します。

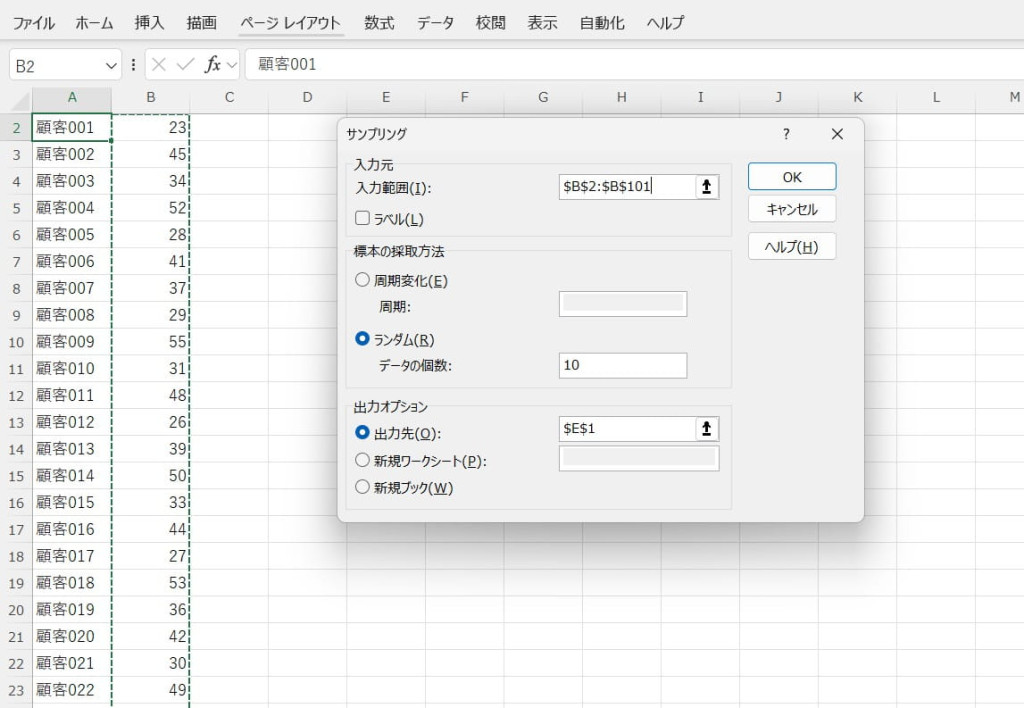
抽出されたサンプルを確認して分析に使用します。

Excelの「データ分析」の注意点

Excelのデータ分析機能を使う際は、データ量、更新性、セキュリティの3点に注意が必要です。ここでは、Excelのデータ分析の注意点について解説します。

データ量を制限する

Excelのデータ分析機能では、扱うデータの量が多すぎると動作が重くなり、フリーズしてしまう恐れがあります。そのため、分析の目的に応じて、必要なデータだけを抽出して扱うようにしましょう。

データが自動で更新されない

Excelでは、分析結果が出力された後に分析対象のデータに変更を加えても、分析結果は自動で更新されません。そのため、対象データを更新した場合は、分析の手順を最初からやり直す必要があります。

セキュリティとプライバシーの対策が必要

悪意のあるマクロが含まれたExcelファイルを開くと、ウイルス感染などのリスクがあります。そのため、ウィルス対策ソフトなどでチェックした上でファイルを開いたり、機密データは適切に保護したりするなどの対策が必須です。

Excelのデータ分析を効果的に使おう！

Excelのデータ分析機能は、誰でも効率的に本格的なデータ分析が可能です。平均や分散といった基本統計から回帰分析、フーリエ解析まで、幅広い分析が行えます。また、売上データの傾向把握、実験結果の検定、業務効率化など、幅広い分野で利用されています。目的に応じてExcelの分析機能を使い分けることで、データの価値を最大限に引き出せます。

Excelのデータ分析についてさらに詳しく学びたい方には、以下の講座がおすすめです。

◆【すぐ実践できる！】Excelデータ分析/統計解析 超入門コース【3時間速習】

レビューの一部をご紹介

評価：★★★★★
コメント：データ分析の超入門ということでしたが、初学習者としては非常に難しい内容だったなと感じる反面、それを難しいと感じさせないわかりやすい説明であったというのが正直な感想です。反復することで分析力が高められそうなので、引き続き動画を繰り返し見させていただきます！

評価：★★★★★
コメント：非常に分かりやすいです！技術面に触れつつも、実践を重視した素晴らしい講座です。講座で使用したExcelファイルがダウンロードできるのもありがたい。

◆PythonとExcelで学ぶデータサイエンス入門：確率分布の実践的アプローチ

Excelのデータ分析機能を効果的に使って、様々なデータを効率的に分析しましょう！