パーセプトロンとは？機械学習のルーツをPythonを使って徹底解説

パーセプトロンとPythonの組み合わせで機械学習を学びたいと思っているが、

・パーセプトロンのアルゴリズムが理解できない…。
・ Pythonでの実装方法が分からない…。

という方も多いのではないでしょうか？

この記事では、

・ パーセプトロンの基本的なアルゴリズム
・Pythonを使用した具体的な実装方法

について詳しく解説します。

公開日：2023年11月28日

パーセプトロンとは信号出力のアルゴリズム

パーセプトロンは、コンピュータが物事を判断するためのシンプルなルールの一つです。イメージとしては、質問に「はい」か「いいえ」で答えるクイズゲームのようなものです。

例えば、「りんごは赤いですか？」という質問に対して、りんごが赤いなら「はい」、赤くないなら「いいえ」と答えますよね。パーセプトロンも同じように、いくつかの質問に「はい」か「いいえ」で答えて、最終的に何かを判断します。

ただし、パーセプトロンはとてもシンプルなので、答えが「はい」か「いいえ」の質問しかできず、複雑な判断は苦手です。

例えば、「りんごはおいしいですか？」という質問は、人によって意見が違うため「はい」か「いいえ」で答えるのが難しいです。

このシンプルなルールをたくさん組み合わせることで、コンピュータはもっと複雑な判断をすることができるようになります。それが、パーセプトロンを使った学習の基本です。

パーセプトロンは機械学習において重要な役割を果たすアルゴリズムで、その中には様々な種類が存在します。

それらの種類はパーセプトロンの中で細分化されており、それぞれ異なる特徴を持っています。

パーセプトロンのアルゴリズム発展の流れ

ここでは、パーセプトロンのアルゴリズムの中でも基本的な形式ニューロンから、

・単純パーセプトロン
・多層パーセプトロン
・ニューラルネットワーク

に至るまでの流れを解説していきます。

形式ニューロン：脳の神経細胞の数理モデル

形式ニューロンは、脳を構成する神経細胞、すなわちニューロンを数理モデル化したものです。

このモデルでは、複数の入力を受け取り、それらを細胞体で加算し、ある閾値を超えたら出力するという仕組みを持っています。

関数で表すと、入力の合計が正であれば1を、負であれば0を出力する単純な関数になります。

この形式ニューロンの概念は、単純パーセプトロンへと発展していきます。

単純パーセプトロン：いくつかの入力信号から1つの値を出力

単純パーセプトロンは、複数の入力信号を受け取り、それらを加重和して、ある閾値（しきいち）を超えたら1を、超えなければ0を出力する仕組みを持っています。

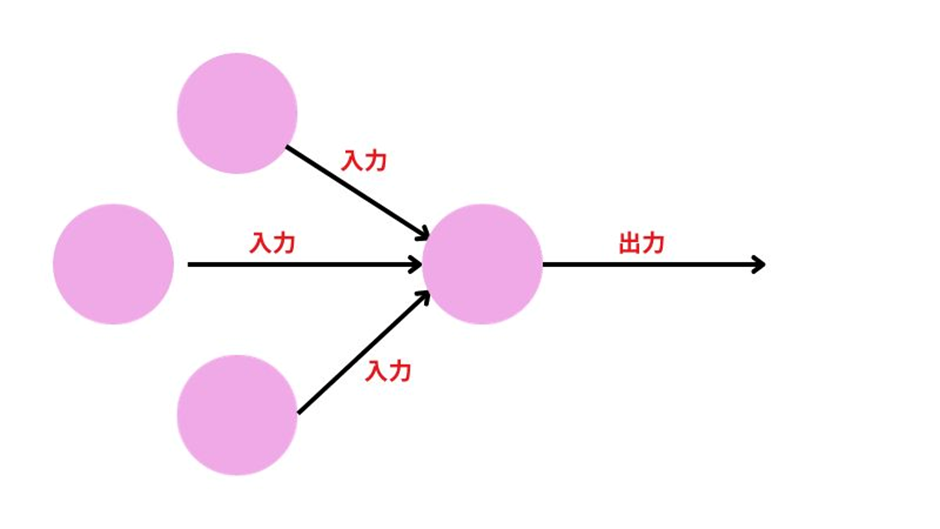
※単純パーセプトロンのイメージ図

この単純パーセプトロンは現在でも広く使われており、本記事ではPythonを使って単純パーセプトロンを実装する方法を後述しています。

ただし、単純パーセプトロンは直線で分けられない問題には対応できない、という点に注意が必要です。

限界を克服するために、単純パーセプトロンが多層化されたものが多層パーセプトロンです。

多層パーセプトロン：単純パーセプトロンが多層化されたもの

多層パーセプトロンは、単純パーセプトロンを多層にしたもので、より複雑な問題を解くことができます。

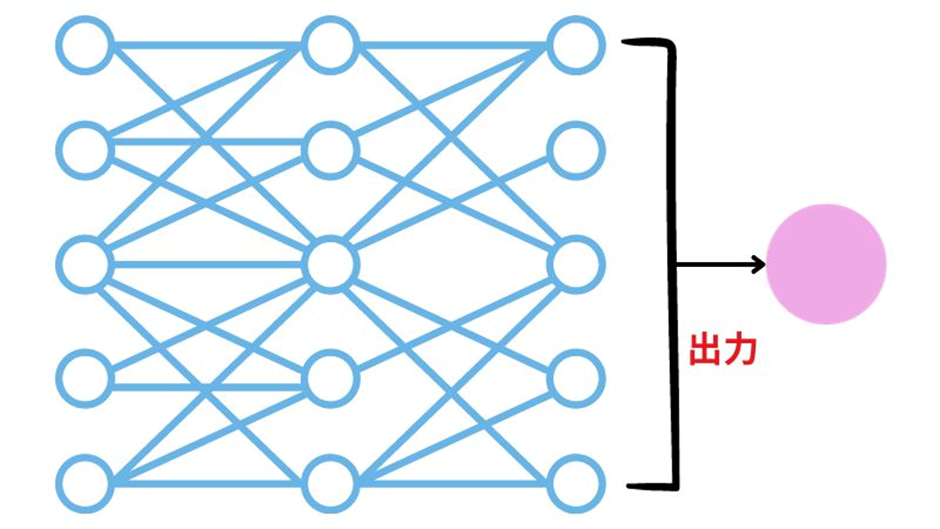
※多層パーセプトロンのイメージ図

特に、直線で分けられない問題に対しても対応可能であり、未来のデータを予測する回帰問題にも利用することができます。

この多層パーセプトロンの概念をさらに発展させたものがニューラルネットワークです。

ニューラルネットワーク：多層パーセプトロンを発展させたもの

ニューラルネットワークは、多層パーセプトロンの仕組みをさらに発展させたもので、単純な関数を組み合わせることによって非常に複雑な関数を表現することができます。

これにより、線形な問題だけでなく、非線形な問題にも対応することが可能になります。 ニューラルネットワークについてさらに詳しく知りたい方は、「ニューラルネットワークとは？人工知能の基本を初心者向けに解説！」を参照してください。

パーセプトロンの3つの論理回路

パーセプトロンは単純ながらも強力な計算能力を持っており、基本的な論理演算を行うことができます。

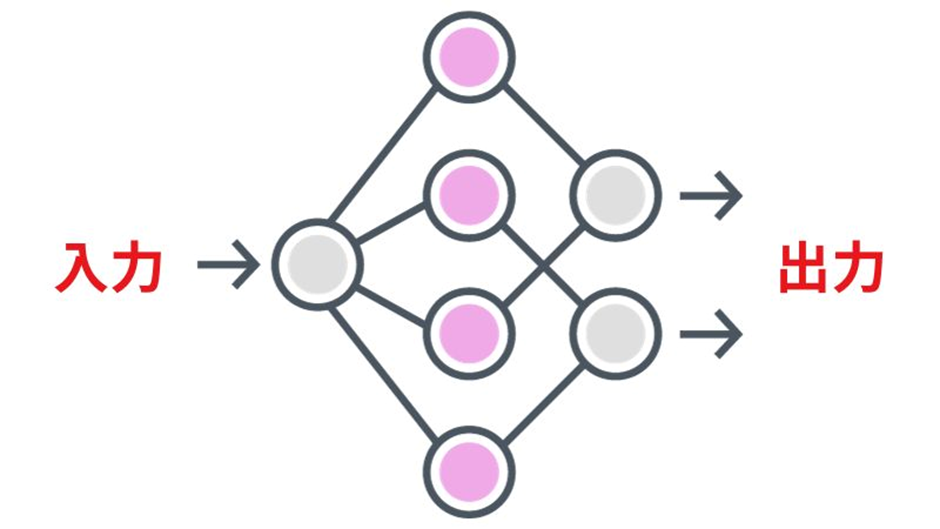
※ニューラルネットワークのイメージ図

ここではパーセプトロンを用いて、実現可能な3つの基本的な論理回路について解説します。

①論理積(AND)

ANDゲートは「…かつ…」を意味する論理回路で、入力された2つの信号がともに1のときのみ1を出力し、それ以外の場合は0を出力します。

これは論理的な「かつ」の条件を満たすため、両方の条件が真である必要があります。

②否定論理(NAND)

NANDゲートは「…でない」を意味する論理回路で、入力された2つの信号がともに1のときだけ0を出力し、それ以外の場合は1を出力します。

この単純な論理回路を基に、他の論理回路を構築することが可能です。

③論理和(OR)

ORゲートは「…または…」を意味する論理回路で、入力された2つの信号のうち少なくとも1つが1であれば1を出力し、両方とも0の場合のみ0を出力します。

これは論理的な「または」の条件を満たし、どちらか一方または両方が真であればよいという特性を持っています。

これらの論理回路は非常に単純ですが、それぞれを組み合わせることでより複雑な計算を行うことが可能です。

パーセプトロンを用いてこれらの論理回路を実装することで、機械学習の基礎を学ぶことができます。

パーセプトロンをPythonで論理回路を使って実装する方法

パーセプトロンは単純ながらも強力な計算能力を持ち、基本的な論理演算を行うことができます。

ここでは、Pythonを使用してパーセプトロンを用いた論理回路、具体的にはANDゲート、NANDゲート、ORゲートを実装する方法について解説します。

ANDゲートで実装

ANDゲートは「AかつB」、つまり「Aであり同時にBである」を意味する論理演算機能を持った回路です。

PythonでANDゲートを実装すると、以下のようになります。

このコードでは、AND_gateという関数を定義しています。

関数は2つの入力「x1」と「x2」を受け取り、両方とも「1」のときだけ「1」を返し、それ以外のときは「0」を返します。

NANDゲートで実装

NANDゲートは「NOT AND」を意味し、ANDゲートの出力を反転させたものです。

PythonでNANDゲートを実装すると、以下のようになります。

このコードでは、NAND_gateという関数を定義しています。

関数は2つの入力「x1」と「x2」を受け取り、両方とも「1」のときだけ「0」を返し、それ以外のときは「1」を返します。

ORゲートで実装

ORゲートは「論理和」を意味する論理回路で、入力信号がすべて「0」のときだけ出力Yが「0」となり、それ以外の場合はすべて出力が「1」になります。

PythonでORゲートを実装すると、以下のようになります。

このコードでは、OR_gateという関数を定義しています。

関数は2つの入力「x1」と「x2」を受け取り、少なくとも1つが「1」であれば「1」を返し、両方とも「0」であれば「0」を返します。

パーセプトロンを使う上での注意点

パーセプトロンは単純ながらも強力なモデルであり、多くの問題に対して効果的に利用することができます。

しかし、その単純さゆえにいくつかの制限も存在します。

ここでは、パーセプトロンを使用する際に注意すべき点について解説します。

2クラスしか分類できない

パーセプトロンは、基本的に2クラスの分類問題にしか対応していません。

つまり、データセットが2つのクラスに分けられる場合にのみ適用可能です。

もし、2クラスがデータ空間上で混在している場合、パーセプトロンはうまく決定境界を引くことができません。

この制限を克服するためには、より複雑なモデルやアルゴリズムを使用する必要があります。

線形分離不可能な問題は学習できない

パーセプトロンは線形分離可能な問題、つまりデータを直線（または平面、超平面）で分けることができる問題に対してのみ効果的です。

線形分離不可能な問題、例えば単純な線形分離では解決できないXOR問題(排他的論理和)などに対しては、単一のパーセプトロンでは解を見つけることができません。

しかし、複数のパーセプトロンを組み合わせることで、非線形問題に対しても対応することが可能になります。

これが多層パーセプトロンやニューラルネットワークへと、発展していくきっかけとなりました。

パーセプトロンとPython実装のエッセンスを理解しよう！

この記事では、パーセプトロンの基本的な概念とその種類、そしてPythonを使用した具体的な実装方法について解説しました。

パーセプトロンは、単純ながらも強力な機械学習のモデルであり、2クラスの分類問題において効果を発揮します。

しかし、その単純さゆえに線形分離不可能な問題には対応できない、という制限もあります。

制限を克服するためには、パーセプトロンを組み合わせることで複雑な問題に対応可能なモデルを構築する必要があります。

Pythonを使ったモデルの実装について学びたい人には、下記の講座がおすすめです。

レビューの一部をご紹介

評価：★★★★★
このコースは非常に充実しており、期待以上の価値がありました。LLMモデルや生成系AIの概念を理解することができました。特にAPIを用いたコーディングの実演は非常に役立ちました。この内容は実務でAPIを使用してコーディングをするときに役立つものと感じました。理論と実践の両面をバランスよく学ぶことができ、将来のプロジェクトに活かせるスキルを身につけることができました。これから受講する方にも強くお勧めします。

評価：★★★★★
複数のパーセプトロンを重ねることで表現力が上がるということがよくわかりました。

Pythonを使いこなしてパーセプトロンや機械学習の知識を効率的に取得しましょう！