エクセルでt検定を使おう！分析ツールを使った簡単な方法を紹介

統計を学び始めると、様々な検定方法が登場してきます。知識として学ぶだけではなかなか身に付かないと感じ、実際に自分で検定をしてみたい！という方も多いのではないでしょうか。
検定で有名なt検定を手計算でやるには、ルートの計算などが複雑で嫌気が差してしまいます。

そんな時に役に立つのがエクセルです。エクセルにはt検定を行うための関数が備わっているため、関数を使えばあっという間にt検定ができます。

この記事ではエクセルで便利にt検定を行う方法をご紹介します。t検定について詳しく解説した記事もありますので、ぜひご参照ください。

t検定をエクセルで行う前に確認しておくことは？

t検定は、調べたいデータの平均を使い、そのデータの効果や品質を評価するものです。
詳しくは先ほどご紹介した記事を見ていただくとして、t検定は「データに対応があるとき」と、「データに対応がないとき」の2種類があります。

エクセルで行うt検定は、それぞれ異なる方法で実施していきます。エクセルの分析ツールを使うこともできますが、今回は関数の1つである「TEST関数」を使います。

t検定：データに対応のある場合とは？

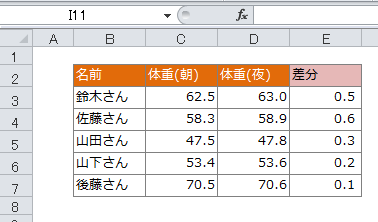
t検定で対応のある場合とは、同じ人やモノで2回計測したデータの差を評価する場合を指します。

具体例：あるグループのメンバーの朝と夜の体重差

t検定：データに対応のない場合とは？

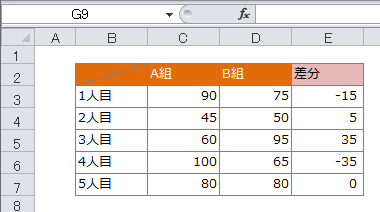
一方、t検定で対応のない場合とは、違う人やモノで計測したデータの比較を評価する場合を指します。ちなみに、データの平均にデータが集まっているかを示す分散が同じか違うかによって、使う分析方法が異なります。（方法については後述します）

具体例：A組とB組の国語のテスト結果

エクセルを使ったt検定のやり方①（対応のある場合）

それでは実際に、対応のある場合のエクセルのt検定方法をご紹介していきます。データは先ほどの朝と夜の体重差の表を利用します。

準備

エクセルのメニューに「分析ツール」が無い時は、下記の手順で表示することができます。

①1番左上にある「ファイル」を開き、「オプション」をクリックします。

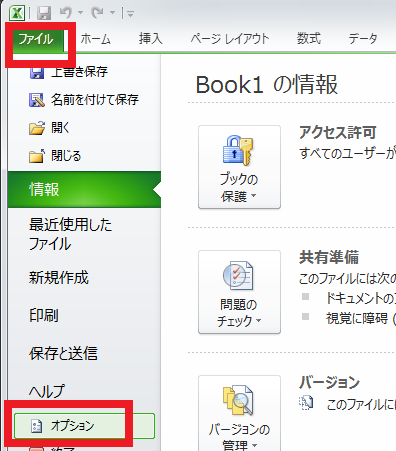
②「アドイン」をクリックし、「分析ツール」の管理欄がExcelのアドインになっている状態で「設定」をクリックします。

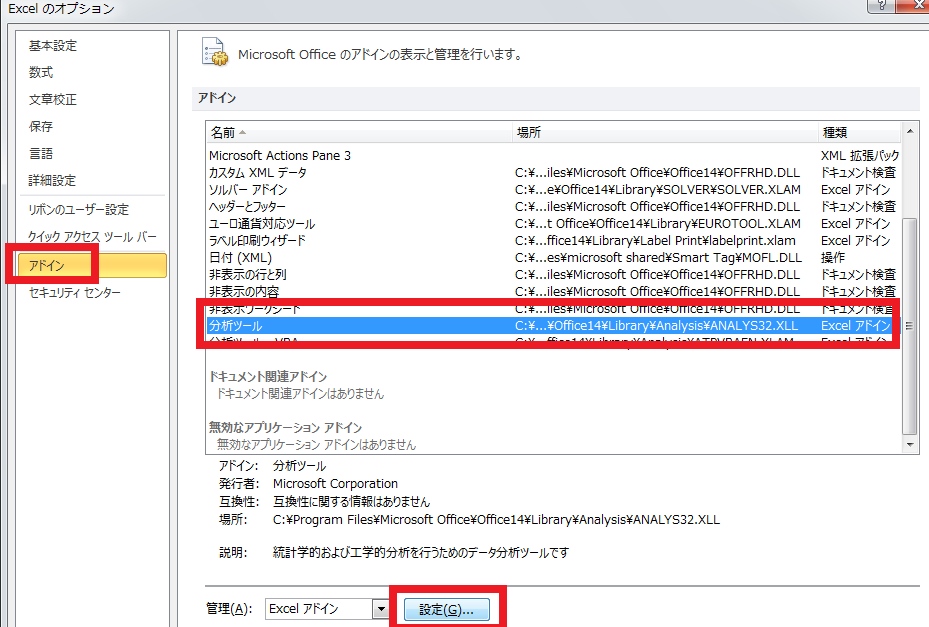
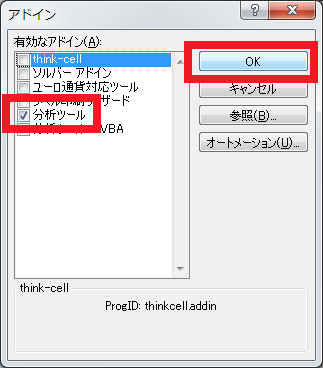
③「分析ツール」にチェックを入れて「OK」をクリックします。

t検定の方法（対応のある場合）

それでは実際にエクセルの分析ツールを使ってt検定を行っていきましょう。

①「データ」から「データ分析」を開きます。

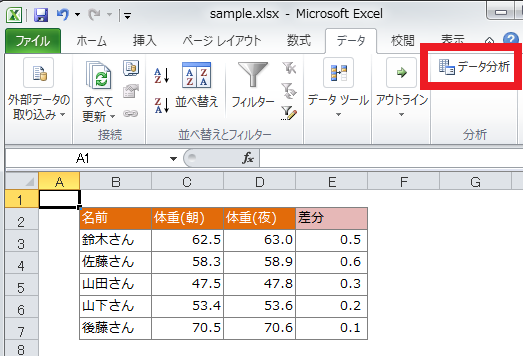
②「t検定：一対の標本による平均の検定」を選択し「OK」をクリックします。

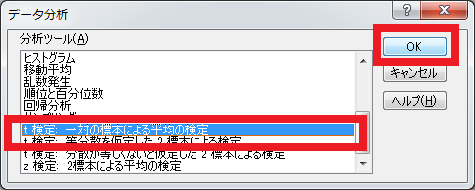
③入力画面が表示されるため、それぞれ値を入力していきます。

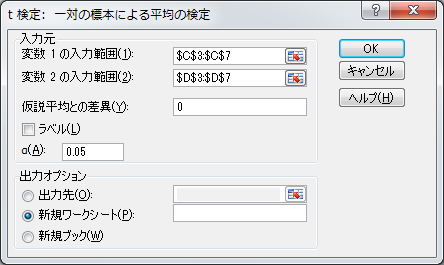
変数1の入力範囲：体重(朝)のデータ範囲
変数2の入力範囲：体重(夜)のデータ範囲
仮説平均との差異：2つのデータの意味は同じという0を入力
α：有意水準(データの傾向がずれる割合)5％の検定

エクセルを使ったt検定の結果（対応のある場合）

下記のような結果が表示されました。双方向で検証する両側検定の場合は、t値、P(T<=t) 両側、t 境界値 両側を確認していきます。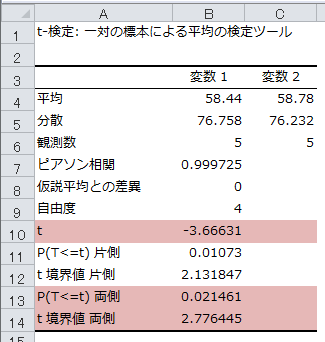

ｔ境界値両側（両側検定で有意差が認められる境界値）が2.7…となるのに対して与えられたデータから計算したｔ値が-3.66…となり、ｔ値が境界値よりも大きくなっています。
P(T<=t) 両側も0.05以下になっていることから、2群のデータが等しいという仮説の域に落ちないため、帰無仮説は棄却され「有意差は認められる」、つまりデータは同じ傾向にはないということがわかりました。

※用語がわからない方はt検定について詳しく解説した記事を参考にしてみてください。

ワークシート関数を使ったt検定

エクセルにあるTTEST関数を使うことでもt検定を実施することができます。今回は下記の関数を入力することで同じ結果が得られました。

=T.TEST(C3:C7,D3:D7,2,1)

※C3:C7:体重(朝)のデータ範囲、D3:D7:体重(夜)のデータ範囲、2:両側検定、1:対応のある場合)

こちらは、こういうやり方もあるという程度で、頭に入れておきましょう。

エクセルを使ったt検定のやり方②（対応のない場合）

次に、対応がない場合のエクセルのt検定方法をご説明します。

t検定方法（対応のない場合）

①「データ」から「データ分析」を開き、「t 検定：等分散を仮定した2標本による検定」を選択し「OK」をクリックします。

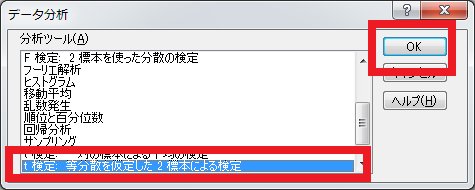
②先ほどと同じようにデータを選択して、「OK」をクリックします。

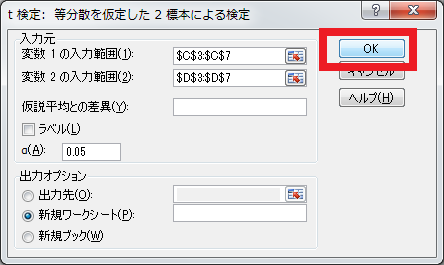
エクセルを使ったt検定の結果（対応のない場合）

下記のような結果が表示されました。双方向で検証する両側検定の場合は、t値、P(T<=t) 両側、t 境界値 両側を確認していきます。

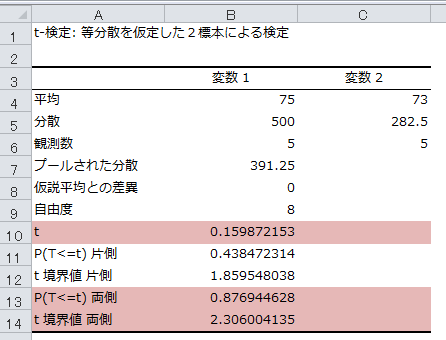
t境界値両側（両側検定で有意差が認められる境界値）が2.3…となるのに対して与えられたデータから計算したｔ値が0.15…となり、ｔ値が境界値よりも小さくなっています。
P(T<=t) 両側も0.05以上になっていることから、2群のデータが等しいという仮説の域に落ち、帰無仮説は棄却されず「有意差は認められない」、データは同じ傾向にあるということがわかりました。

t検定で等分散か不等分散を見極める！f検定とは

f検定とは、比較するデータ群のばらつきが等しいかを評価するものです。

データ群によっては「分散が異なるかどうか」がわからない場合があります。その場合は「分散が異なることを仮定したt検定」をそのまま使うのがセオリーです。

このf検定は、分散の状況により結果が変わるt検定の前にやっておくといいでしょう。f検定もt検定と同じような方法で評価することができます。

t検定はビジネスの場面で役立つことも多い検定手法です。しっかり理解し、仕事に役立てていきましょう。