仮説検定とは？計算の手順や用語をわかりやすく解説！

仮説検定について学び始めたものの、

・仮説検定に関連する用語の意味が理解できない…。
・計算手順などがよく分からない…。

という方もいるのではないでしょうか。

そこでこの記事では、統計学の初心者向けに

・仮説検定の目的や用語の意味
・仮説検定の計算方法

について具体例を交えながら解説します。

仮説検定とは

仮説検定とは、ある仮説が正しいか否かについて統計学的に検証する手法です。より厳密には、母集団に関するある仮説の真偽について、母集団から得られた標本をもとに確率的に判断する統計手法を仮説検定と呼びます。

例えばマーケティング分野では、広告が商品の売上と関連しているかどうかの判断に仮説検定を使うことが可能です。仮説検定では、まず「ある商品の広告と売上の増加には関係がない」という仮説を立てた上で計算を進め、仮説を否定する結果を得ることによって、広告と売上の相関関係を統計的に示します。

仮説検定で用いられる方法のひとつであるt検定については、 「統計の中でも最重要分野のひとつ、t検定について徹底解説！」 ご確認ください。

仮説検定の手順

仮説検定では、いくつかのステップで計算を進めることで仮説の真偽を検証します。具体的な手順は次の通りです。

1. 帰無仮説・対立仮説を立てる
2. 有意水準を設定する
3. 検定統計量に基づいてp値を計算する
4. 帰無仮説を棄却・採択する

1.帰無仮説・対立仮説を立てる

まず始めに、真偽を検証したい事象について、「帰無仮説」と「対立仮説」と呼ばれる2つの仮説を設定します。帰無仮説は、仮説検定において計算の対象となる仮説です。仮説検定を通じて最終的に主張したい内容とは反対の仮説を指します。

例えば、ある広告が商品の売上増加に貢献していることを主張したい場合、帰無仮説は「ある広告と商品の売上増加には関係がない」という仮説です。この帰無仮説の誤りを統計的に証明することで、主張したい内容の正しさが証明できます。

一方、対立仮説とは帰無仮説と対立する仮説のことです。帰無仮説が「ある広告と商品の売上増加には関係がない」というものであれば、その反対の「ある広告と商品の売上増加には関係がある」という仮説が対立仮説となります。

2.有意水準を設定する

有意水準とは、仮説検定において帰無仮説が誤っているか否かを判断するための基準です。帰無仮説として設定した事象が起こる確率を計算した結果が有意水準よりも低かった場合に、帰無仮説は誤りであると判断されます。

有意水準の値としては、0.05（5%）または0.01（1%）を用いることが一般的です。例えば、有意水準を0.05として仮説検定を行う場合、帰無仮説が起こる確率の計算結果が5%未満となったときに誤った仮説だと判断します。

3.検定統計量に基づいてp値を計算する

次に、検定の対象となるデータから「検定統計量」を算出します。検定統計量とは、実際に観測されたデータ（標本）をもとに、ある事象が起こる可能性を数値として表したものです。検定統計量は数学における確率という概念に似ているものの、厳密な定義は異なります。

例えば、サイコロを1回振って何の目が出るかといった事象の場合、出る目のパターンは1から6の6通りしか存在しないため、確率の計算が可能です。しかし、広告と商品の売上の増加に関係があるかといった事象では、いくら売上が増えるかに無数のパターンがあるため、サイコロの場合のように確率を求めることはできません。

そこで、確率が求められない事象についても、それが起こる可能性を数値化するために検定統計量という考え方を用います。ある事象について観測したデータから検定統計量を算出する方法は、行う検定の手法によって様々です。

代表的な検定統計量として、次のようなものが挙げられます。

t値

t値は、母集団の平均値について検証するt検定で用いられる検定統計量です。2つの集団の平均値に差があるかなどを調べる際に、t値を算出します。

f値

f値は、母集団の分散に差があるかどうかを検証するF検定で用いられる検定統計量です。分散とはある集団におけるデータのばらつきを数値化したものです。2つのグループの分散を比較する際に、f値を算出します。

カイ二乗値

カイ二乗値は、独立性の検定や適合度検定で用いられる検定統計量です。独立性の検定とは、いくつかのカテゴリに分けられるデータに対して、2つの変数間に相関関係があるかどうかを判断する手法を指します。

例えば、広告を出した・出さなかった、売上が上がった・上がらなかったなどにカテゴリ分けしたデータについて、広告の有無と売上の変化に関係があるかを調べることが可能です。適合度検定では、あるグループにおける男女比など、カテゴリ分けされたデータに関する数値が理論上の数値と合っているかを調べられます。

仮説検定では、目的に応じて検定統計量を計算したあと、p値と呼ばれる数値を求めます。p値とは、確率分布において検定統計量よりも外側の値が観測される確率のことです。つまり、観測した事象と同じか、それよりも極端な事象が起こる可能性を表します。ある事象について求めたp値が小さいほど、その事象が起こる可能性は低いと判断することが可能です。

検定統計量は、種類によって値の大きさが異なるため、大小を単純に判断することができません。検定統計量をp値に変換することで、判断基準を検定の手法によらず統一し、仮説検定を進められるようになります。

4.帰無仮説を棄却・採択する

最後に、p値と有意水準を比較し、帰無仮説の棄却または採択の判断を行います。棄却とは、立てた仮説が誤っていると判断し否定することです。反対に、採択とは仮説を正しいと認めることを指します。

これまでの手順で求めたp値が有意水準よりも小さい場合、帰無仮説を棄却し、対立仮説を採択します。例えば、「ある広告と商品の売上増加には関係がない」という帰無仮説について、p値があらかじめ定めた有意水準（0.05や0.01など）より小さければ、この仮説は誤りです。そして、「ある広告と商品の売上増加には関係がある」という対立仮説が正しいと判断できます。

一方、p値が有意水準よりも大きい場合は、帰無仮説は棄却されず、対立仮説が正しいという判断はできません。

仮説検定の注意点

仮説検定を実施する際には、仮説の設定方法や結果の判断について気を付けるべきポイントがあります。仮説検定の主な注意点は次の通りです。

主張したい仮説を対立仮説に設定する

仮説検定における帰無仮説と対立仮説には、決め方のルールがあります。正しさを主張したい仮説を対立仮説に設定することが必須の条件です。

例えば、ある新薬が有効であることを主張したい場合、「新薬に効果がある」という仮説が対立仮説となります。一方、帰無仮説は「新薬に効果がない」という仮説です。仮説検定の計算を通じて帰無仮説を棄却することで、もともと主張したかった対立仮説が正しいことを示せます。

帰無仮説を棄却しない場合も帰無仮説が正しいとは限らない

仮説検定は、あくまでも対立仮説が正しいことを背理法によって証明する手法です。背理法とは、正しさを主張したい内容についてそれと反対の仮説を立て、仮説が成り立たないことを示す証明方法を指します。

そのため、p値が有意水準より大きく、帰無仮説を棄却できなかった場合でも、帰無仮説が必ずしも正しいとは限りません。正確には、帰無仮説と対立仮説のどちらが正しいのか分からない状態とみなされます。別の標本データを用いて改めて検証を行い、帰無仮説を棄却することも可能です。

具体例で仮説検定を行ってみよう

仮説検定の具体的な計算例として、次のような場合を考えます。

ある商品を販売する企業では、売上を伸ばすために今年度から広告を出し始めた。昨年度までの1日あたりの売上は70,000円で、今年度の無作為に選んだ10日間の平均売上は75,000円だった。この時、広告は売上に貢献していたと判断できるか。ただし、昨年までの1日あたりの売上は期待値70,000円、標準偏差8,000円の正規分布に従っていたものとする。

この例では、平均売上が昨年度の70,000円から今年度の75,000円に増えているという事実から、広告に効果があったように見えます。しかし、今年度の日々の売上という母集団から無作為に選んだ10日間の標本データに、たまたま売上の高かった日が多く含まれていただけで、広告による成果ではないかもしれません。

母平均の検定で仮説検定を行う

このようなケースについて統計的に判断するために、母平均の検定と呼ばれる計算方法で仮説検定を行います。

広告に売上増加の効果があったということを仮説検定で主張するために、その反対の「広告に売上増加の効果がなかった」という帰無仮説を設定します。対立仮説は「広告に売上増加の効果があった」というものです。

有意水準は0.05（5%）とします。これにより、帰無仮説が正しいにもかかわらず誤って否定してしまう可能性を5%という低確率に設定することが可能です。これにより、統計学的に十分な正しさを確保できます。

広告に売上増加の効果がない場合、今年度の1日あたりの売上は昨年度と同じ「期待値70,000円、標準偏差8,000円の正規分布」に従うはずです。母集団がこの正規分布に従う場合、10日間の標本平均（標本の大きさが10）は、「期待値70,000、標準偏差800」の正規分布となり、次のようなグラフとして表されます。

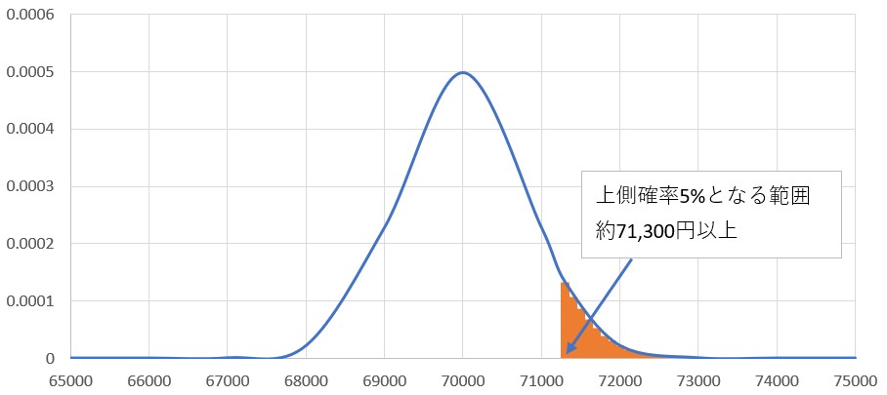
正規分布のグラフは、ExcelのNORM.DIST関数を用いて描くことが可能です。また、NORM.DIST関数による計算で、上側確率が5%となる範囲も算出できます。上記の例では、1日の平均売上が約71,300円以上の範囲に入る確率が5%と計算されました。

しかし、今年度の10日間の標本平均は75,000円であり、帰無仮説が正しい場合における正規分布の上側確率5%の範囲（約71,300円以上）に入っています。つまり、帰無仮説が正しいとするならば確率的には起こりにくいはずの事象が起きていることとなり、帰無仮説の棄却が可能です。

これらの手順で、今年度は広告を出したことにより、前年度よりも1日あたりの平均売上が上がっていることが説明できます。

まとめ

仮説検定は、様々なデータについて統計的な判断を行うための手法です。データをもとに主張したい内容とは逆の仮説を帰無仮説として立て、それを棄却することによって主張の正しさを示します。有意水準の設定やp値の計算などの手順を理解した上で、仮説検定を実施しましょう。

仮説検定についてより詳しく学びたい人には、下記の講座がおすすめです。

レビューの一部をご紹介

評価：★★★★★
コメント： やさしい語り口で、講義のスピードも程良い感じでした。ただの数式だけではなく、図を用いて視覚的にも理解が進むように工夫してありました。

評価：★★★★★
コメント： 見やすい、聞きやすい、わかりやすいがそろっている講座ですね！基本的なことから深いところまで学べます！

仮説検定を学んで、データを正しく分析できるスキルを身につけましょう！