統計学は、一見するとなんの法則も無いかのようなデータから、何らかの傾向を見つけるための学問です。その有用性から、ビジネス、とくにマーケティングでは広く活用されています。
統計学には、複雑な計算が伴うため、使いこなせる人は多くないでしょう。しかし、エクセルを使えば、だれでも手軽に統計処理を行うことができます。
この記事では、代表的な統計処理を、エクセルの分析ツール、または関数を用いる方法に分けてご紹介します。
\文字より動画で学びたいあなたへ/
Udemyで講座を探す >統計分析とは?エクセルを使ってできるって本当?
ばらつきのある複数の要素が集合したデータから、何らかの特徴を見出すための学問が統計学です。また、いくつかの標本を抽出・分析することで、実際には取得が難しい母集団の特徴を把握するためにも、統計学が活用されています。
近年では、企業と顧客・消費者の間に多くの接点が生まれ、膨大なデータを企業が蓄積できるになりました。こうしたデータは「ビッグデータ」と呼ばれ、マーケティングにおける活用方法が模索されています。
統計分析は、ビッグデータからマーケティング手法の策定につながるヒントを見出すためにも活用されている手法です。統計学については、「統計学入門!文系でもわかる基本知識とおすすめの勉強法」の記事で詳しく解説しています。
統計分析では、専門的な分析ツールが活用されていますが、基本的な分析であれば、エクセルでも実施できます。
エクセルの統計分析において一般的なのが、「分析ツール」と「関数」を用いた方法です。以下では、統計分析で代表的な「相関分析」「回帰分析」「t検定」「分散分析」の4つを、分析ツールと関数を用いた方法にそれぞれ分けてご紹介します。
エクセルで分析ツールを読み込む方法
実際に統計手法について学ぶ前に、エクセルで分析ツールを使う方法をご紹介していきます。あらかじめ、以下のような手順で分析ツールを読み込んでおきましょう。
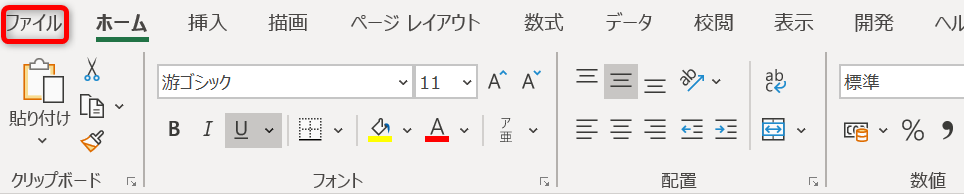
- エクセルを開き、「ファイル」タブをクリックしてください。

- 左下に表示されている「オプション」をクリックします。

- 表示されるオプションメニューから「アドイン」をクリックしてください。

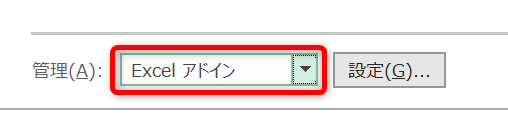
- 「管理」ボックスで「Excelアドイン」を選択し、「設定」をクリックしましょう。

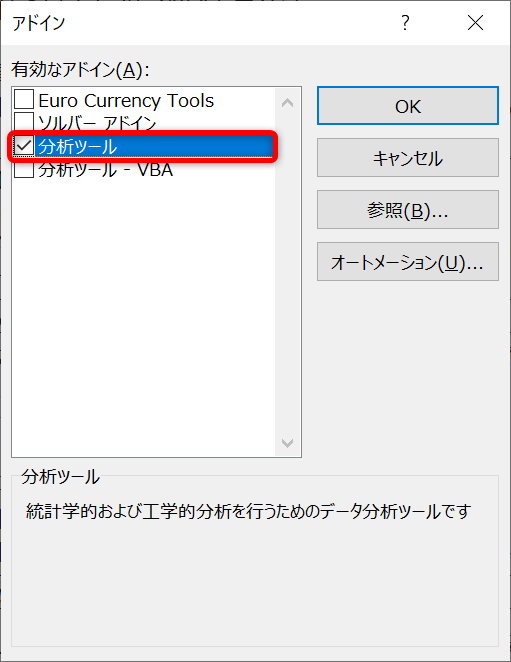
- 「アドイン」ボックスで「分析ツール」にチェックを入れ、「OK」をクリックします。

以上で、分析ツールの読み込みは完了です。
\文字より動画で学びたいあなたへ/
Udemyで講座を探す >エクセルを用いた統計分析①相関分析
相関分析は、2つ以上の要素の変動が関連しているかどうか(相関性)を調べるための分析方法です。例えば「消費者の年齢層」と「商品の売り上げ」が関係しているかどうかや、「店舗の所在地」と「利益率」が関係するかどうか、ということを調べるために使われます。
ビジネスでは、相関分析によって、思わぬ要素が売上に好影響を与えると明らかになり、新たなマーケティングターゲットが見つかることも少なくありません。
具体的に説明すると、相関分析は、要素間の相関係数を求めるための分析手法です。相関係数とは、2つの変量の関連性を示す指標です。-1~1の実数で算出され、1に近いほど、(正の)相関性が強い(1つの要素が増加すると、もう1つも増加する)ことを意味します。また、相関係数が-1に近いほど、負の相関性が強い(1つの要素が増加すると、もう1つは減少する)ことを示します。反対に、相関係数が0に近ければ相関性が弱い(2つの要素は互いに無関係)ということになります。
算出された相関係数の値をどのように解釈するかは、目的にもよりますが、一般的に以下のような目安があります。
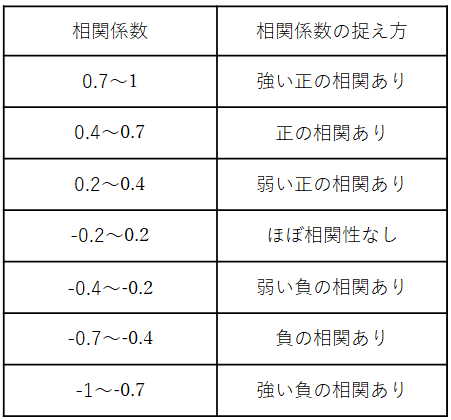
ただし、計算には表れない相関がある場合もあります。そのため、確認として、元データを座標上に記した「分布図」を用いて目視で確認することも大切です。
相関分析~分析ツール編~
エクセルの分析ツールを用いて相関分析を行う方法をご紹介します。
相関関係を調べたいデータをあらかじめ入力しておきます。
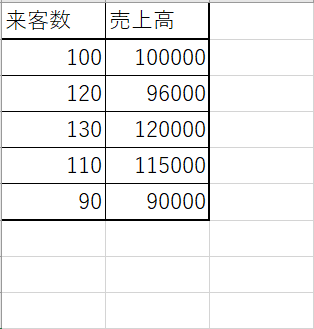
タブから「データ」を選択し、「データ分析」をクリックしてください。

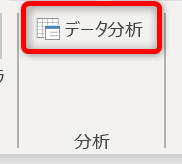
「データ分析」のボックスから「相関」を選択し、「OK」をクリックします。
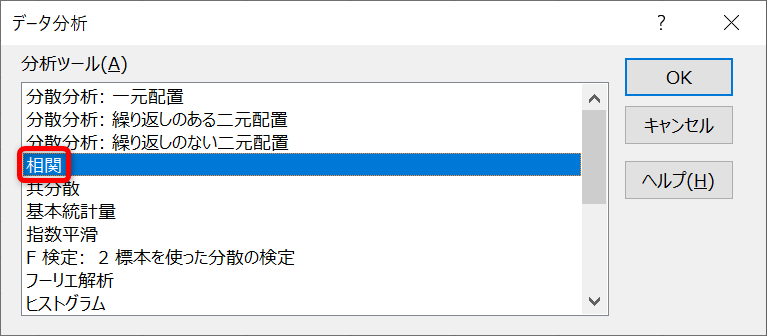
「入力範囲」には相関関係を調べたい数値が入力されたセルの番号を、「出力先」には相関係数を出力したいセルの番号を入れてください。
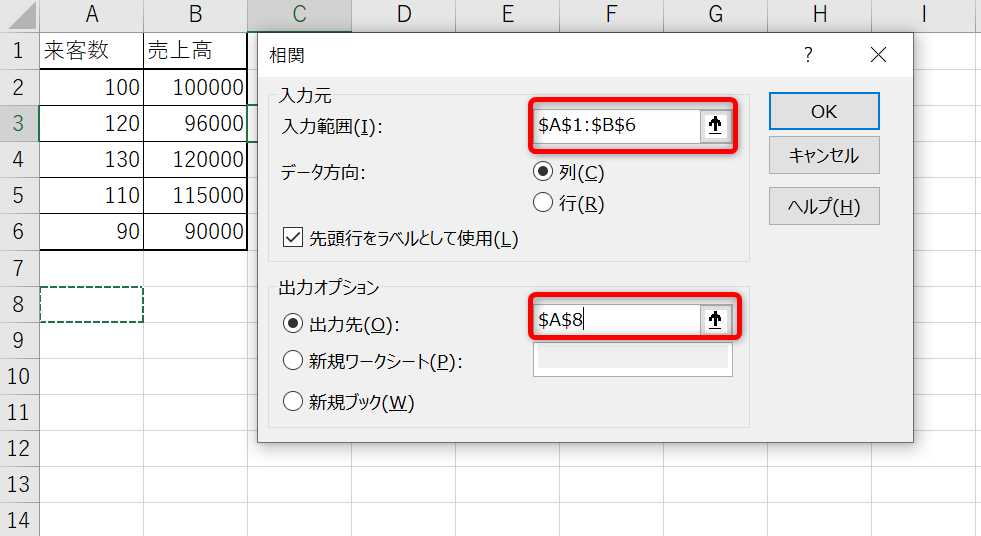
出力先として選択したセルに相関係数が表示されました。
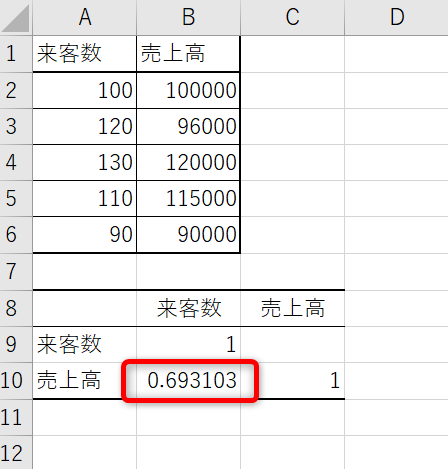
分析ツールを利用した相関分析について、さらにくわしく知りたい方は、「【相関分析】回帰分析との違いやエクセルでの分析、事例を紹介!」をお読みください。
相関分析~エクセル関数編~
エクセルでは、「CORREL関数」を使って相関分析を行うこともできます。
出力先のセルを選択した状態で「CORREL関数」を入力してください。
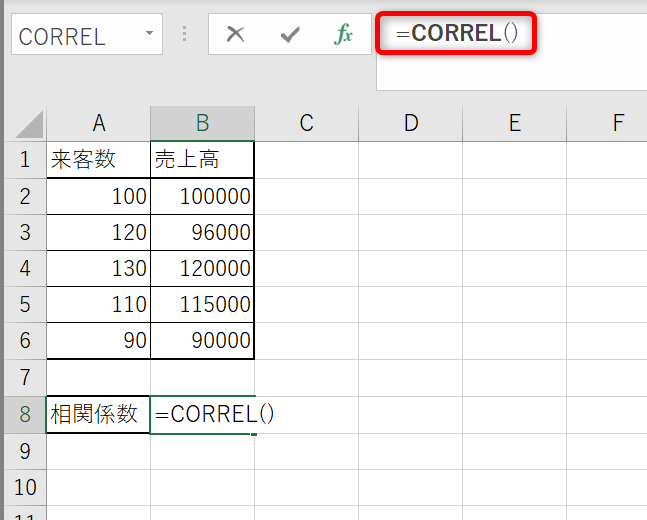
配列には相関関係を確認したい数値が入力されたセルの範囲を指定します。
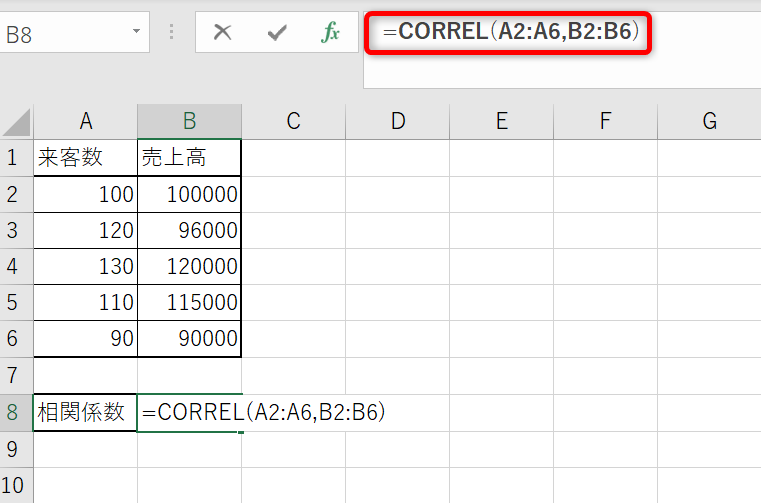
出力先のセルに相関係数が表示されます。
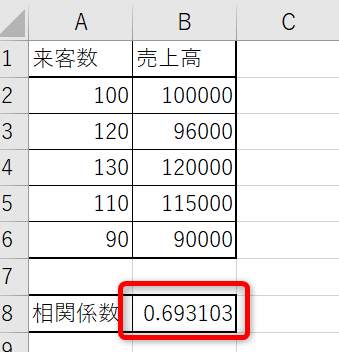
ただし、CORREL関数で求められるのは、2つまでの要素の相関係数です。3つ以上の要素相関関係を調べる場合は、上述したデータ分析を利用する必要があります。
エクセルを用いた統計分析②回帰分析
回帰分析は、ある変数の変動から別の変数の変動を予測・説明するための分析手法です。説明・予測の対象となる変数を目的変数、予測するために用いる変数を説明変数と呼びます。説明変数が1つの場合は単回帰分析、2つ以上の場合は重回帰分析と呼ばれます。
回帰分析を行うと「身長、腹囲、胸囲から体重を予想する」「宣伝費、生産数、リリースからの経過日数から売上を推測する」といったことが可能になります。根拠となるデータが出そろっていない場合も予測できるようになる点がメリットです。一方で、剰余変数の存在に注意しなければ、誤った推論になる可能性があります。剰余変数とは、説明変数以外で、目的変数に影響を与える変数のことです。例えば体重を予想する場合、男性の身長・腹囲・胸囲と体重の関係から立てた式では、女性の体重は求めづらいかもしれません。
回帰分析についてより深く知りたい場合は、「回帰分析(単回帰分析)をわかりやすく徹底解説!」と「ビジネスでもさらに役立つ!重回帰分析についてわかりやすく解説!」をお読みください。
回帰分析~分析ツール編~
まずは、分析ツールを用いた基本的な単回帰分析の方法をご紹介します。
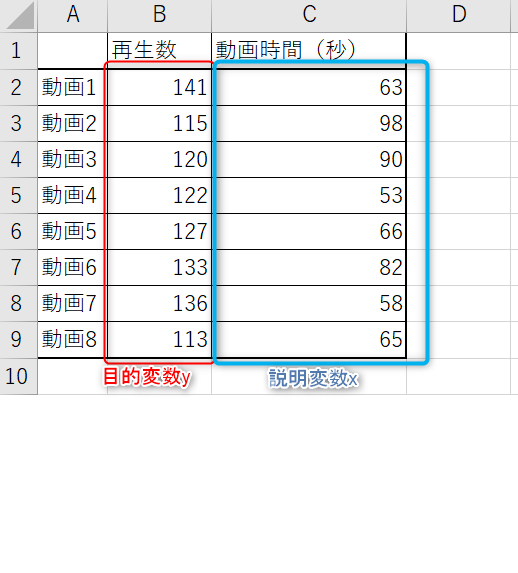
あらかじめ、目的変数と説明変数をセルに入力しておきます。
タブから「データ」を選択し、「データ分析」をクリックしてください。


「データ分析」のボックスから「回帰分析」を選択して「OK」をクリックしましょう。
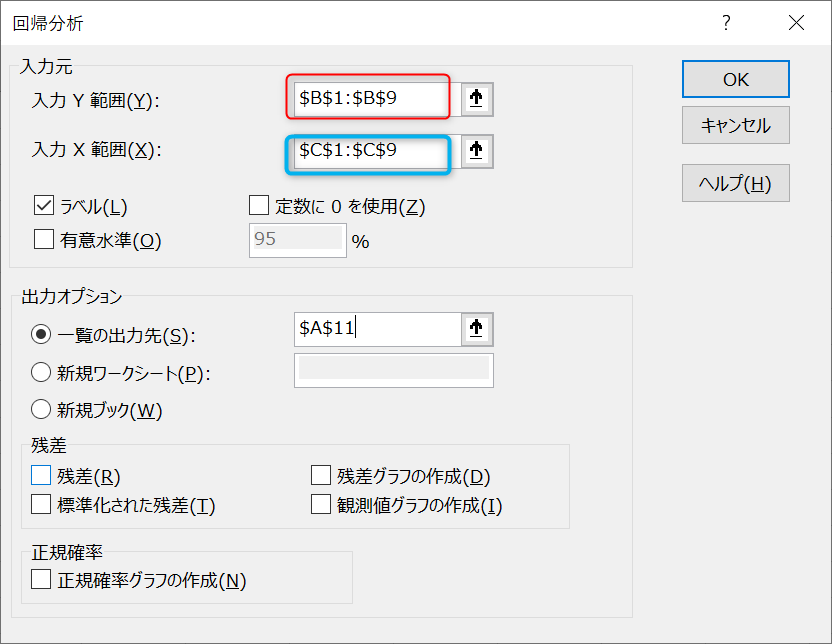
「入力Y範囲」に目的変数の範囲を、「入力X範囲」に説明変数の範囲を指定し、「OK」をクリックしてください。
回帰分析の結果が出力されました。
重回帰分析の場合も大きな違いはありません。「入力X範囲」に、説明変数が入力されたセル全体を指定するだけです。
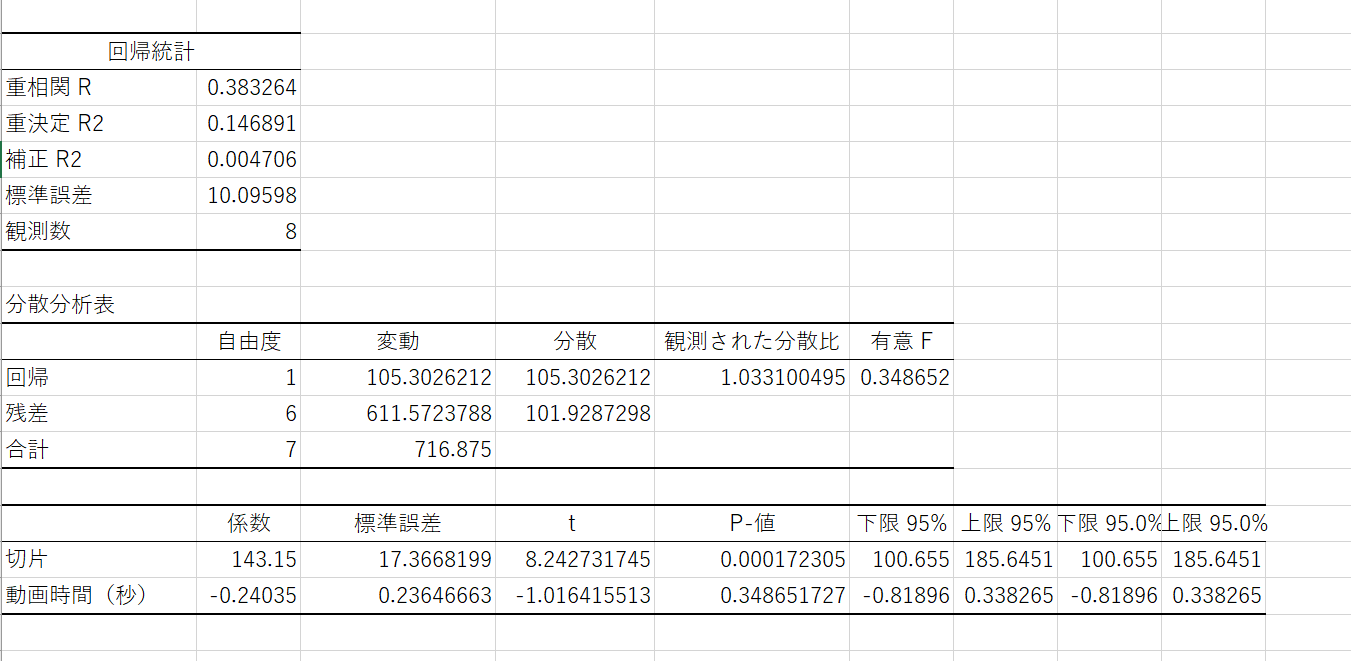
回帰分析の結果としてさまざまな値が表示されていますが、以下では代表的な値の意味を簡単にご紹介します。
重相関R:1に近ければ近いほど、信頼できるデータであることを示す。
重決定R2:重相関Rを2乗した値。1に近ければ説明変数で説明できる割合が多い。決定係数とも呼ばれる。
補正R2:上述した重決定に自由度の影響による補正を加えた実用的な決定係数。
係数:説明変数が目的変数に与える影響の大きさを示す。
回帰分析~エクセル関数編~
関数で回帰分析を行う場合、単回帰分析と重回帰分析で、用いる関数が異なります。また、単回帰分析の場合は係数、切片、決定係数などでも、それぞれ用いる関数が違います。
単回帰分析では、以下の関数を使います。それぞれの関数の用途と、引数として指定する値をご紹介しましょう。
- 係数:slope(目的変数yの範囲, 説明変数xの範囲)
- 切片:intercept(目的変数yの範囲, 説明変数xの範囲)
- 決定係数:rsq(目的変数yの範囲, 説明変数xの範囲)
重回帰分析で用いるのはlinest関数のみです。
関数を入力するセルから縦に5行、横は説明変数の数に1を加えた列数の範囲を指定してください。
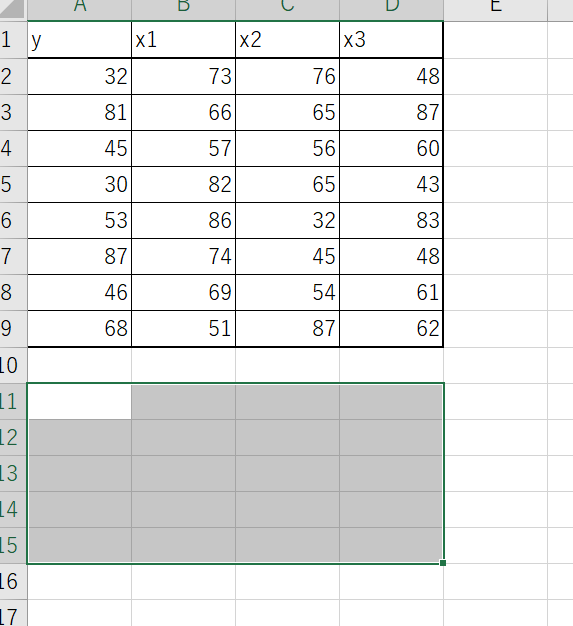
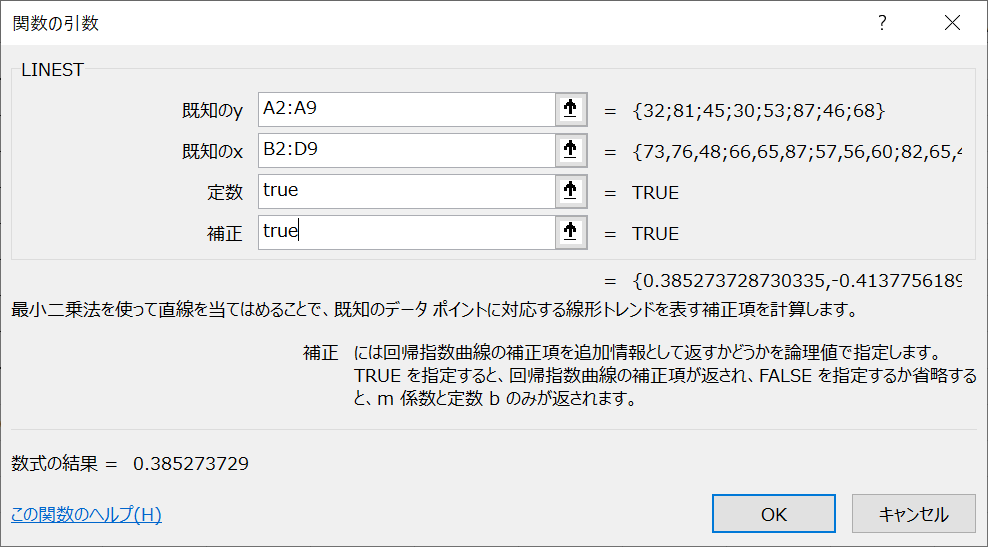
続いてlinest関数を入力します。「既知のy」には目的変数yの範囲を、「既知のx」には説明変数xの範囲を指定しましょう。定数項を含める場合は「定数」に「TRUE」を、標準誤差・決定係数などを含める場合は「補正」に「TRUE」を入力します。
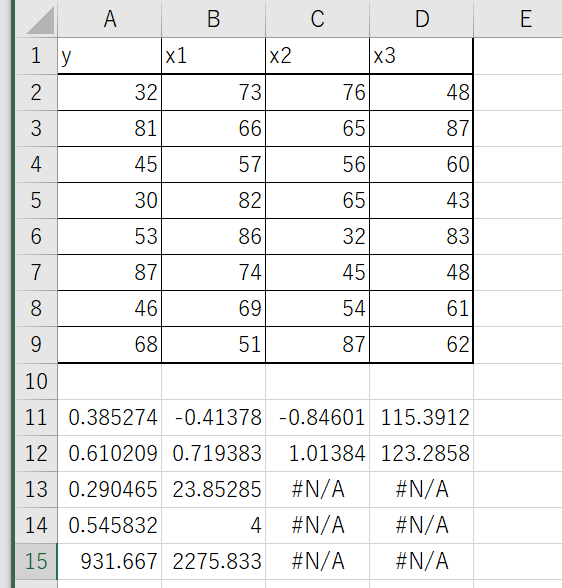
「OK」をクリックすると関数が入力されますが、最初は左端のみに結果が入力されています。結果全体を表示させるためには、「Ctrl」キーと「Shift」キーを押しながら「Enter」を押して関数を入力してください。
エクセルを用いた統計分析③t検定
t検定とは、ある仮説について正否を検討する「仮説検定」で用いられる手法です。母集団から少ないサンプルを抽出し、母集団全体の仮説の正否を検証できるため、さまざまなシーンで活用されています。工業製品の品質管理などで用いられることが多い検定です。
t検定については「統計の中でも最重要分野のひとつ、t検定について徹底解説!」と「エクセルでt検定を使おう!分析ツールを使った簡単な方法を紹介」でくわしく解説しています。
t検定~分析ツール編~
エクセルの分析ツールを用いてt検定を行う場合、「分析ツール」のボックスから「t検定:一対の標本による平均の検定」、もしくは「t検定:等分散を仮定した2標本による検定」を選択し、「OK」をクリックします。
このうち、前者は対応のあるデータ、後者は対応のないデータに対して使用する検定です。対応とは、2つのデータがペアになっているという意味です。例えば、営業チームAの4月の契約件数と5月の契約件数は対応しているといえますが、営業チームAの契約件数と営業チームBの契約件数は、対応しているとはいえません。
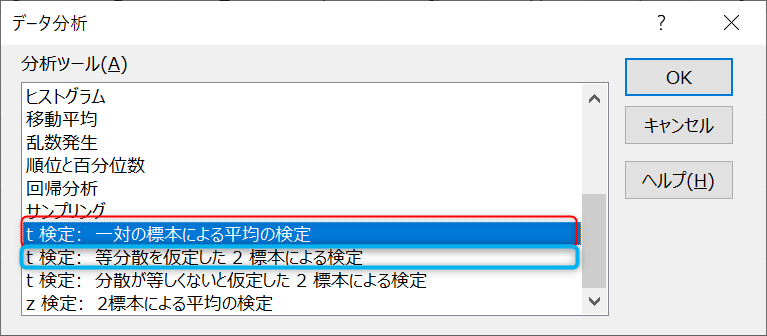
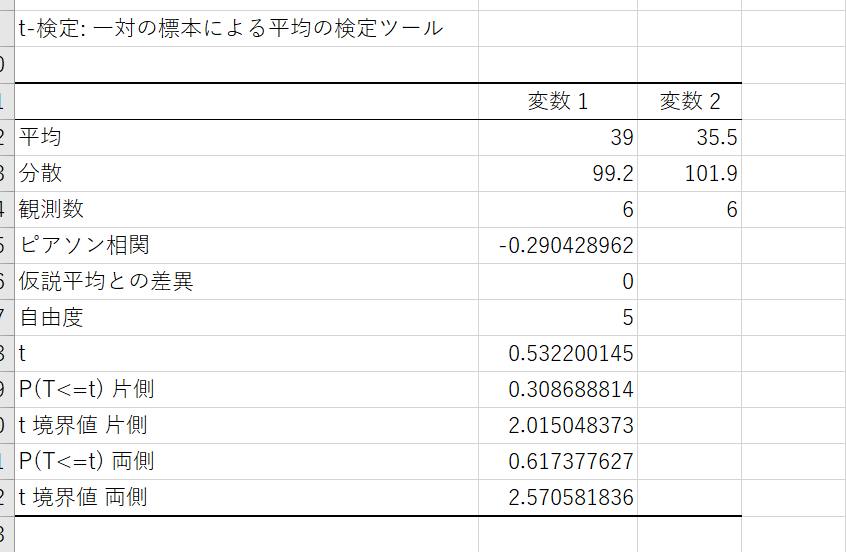
どちらも使い方に大きな違いはありません。対応がある場合は「変数1の入力範囲」に1つ目の条件での標本データを、「変数2の入力範囲」には2つ目の条件での標本データが入力されたセルを指定します。対応がない場合はそれぞれに、2つの標本データが入力されたセルを指定してください。指定が完了したら、「OK」をクリックしましょう。
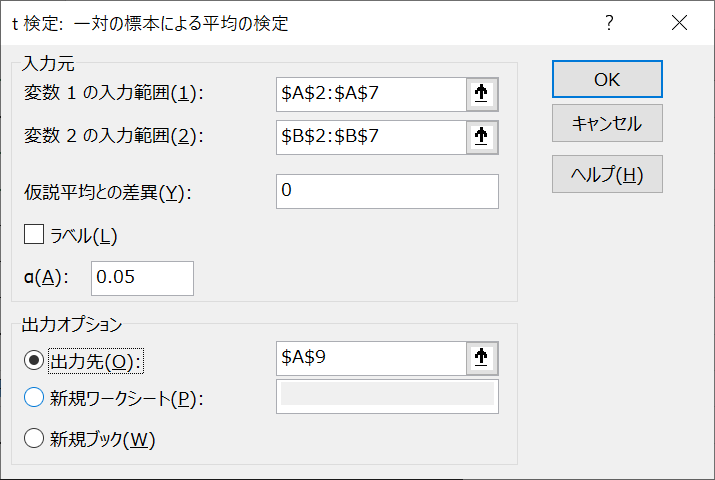
t検定の結果が出力されます。
なお、条件が2つの場合と3以上の場合では分析の設定が異なります。条件が3つ以上ある場合は、「分析ツール」ボックス内の「分散分析:繰り返しのない二元配置」を使用しましょう。
t検定~エクセル関数編~
「T.TEST関数」でも分析ツールのt検定と同じ結果を得ることができます。
結果を出力したいセルに「=T.TEST(条件1の標本データ範囲,条件2の標本データ範囲,2,1)」を入力しましょう。「2」は両側検定、「1」は「対応のある場合」という意味です。
くわしくは「エクセルでt検定を使おう!分析ツールを使った簡単な方法を紹介」をご覧ください。
エクセルを用いた統計分析④分散分析
分散分析とは、3群以上のデータ、もしくは3つ以上の条件下で分類されたデータの母平均の差を検定するための分析方法です。クラスごとのテストの結果や、年間購入額のランクで分けた顧客の年齢など、幅広いシーンで母平均の差を検討するために活用されています。
分散分析を行ううえで知っておかなければならないのが、「要因」と「水準」という2つの概念です。要因は値に変化を与える要素、水準は要因に含まれる項目を意味します。クラスごとのテストの結果に対して分散分析を行う場合、「クラス(組)」という要因のなかに「1組」「2組」「3組」など、クラスの数と同じ数だけ「水準」があることになります。
分散分析では、分析ツールを用いた方法が多く使われます。
分散分析~分析ツール編~
エクセルの分析ツールを用いて、2水準を持つ2要素で構成されたデータに対して分散分析を行う方法を紹介します。
データが下図のように並んでいる場合を考えましょう。
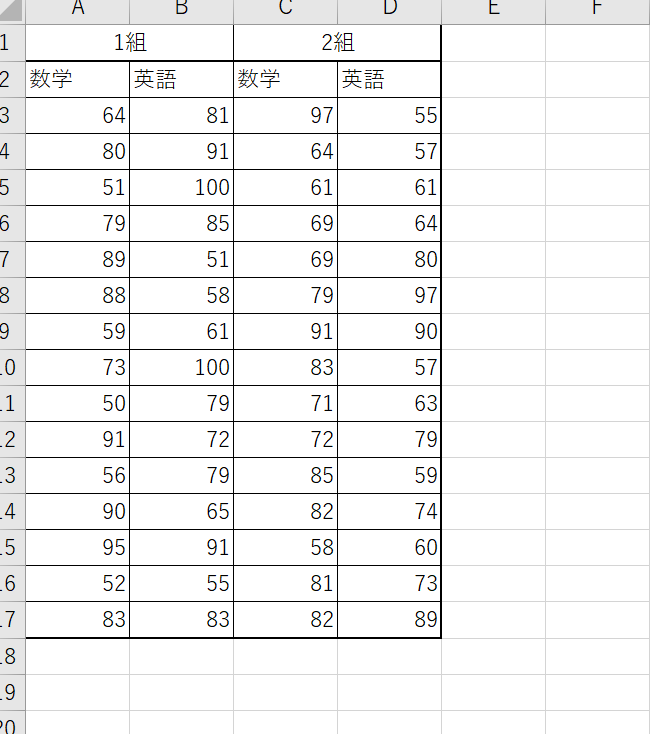
この場合は、下図のような縦長の形に変換してください。
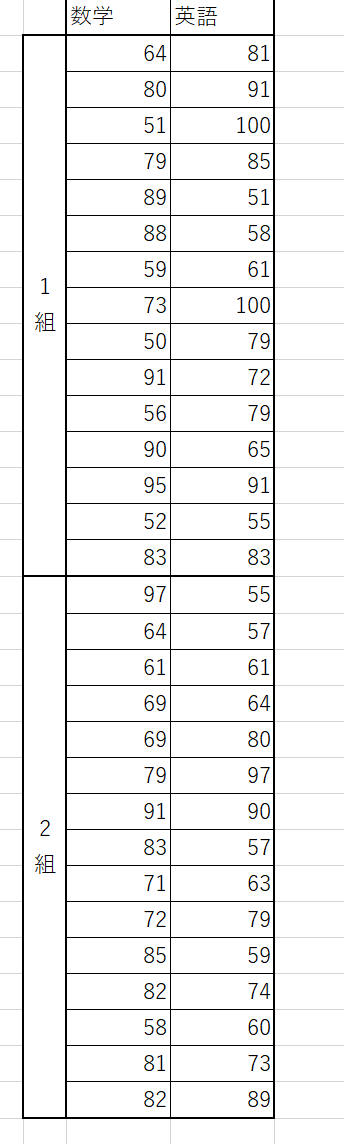
次に、「データ分析」のボックスから「分散分析:繰り返しのある二元配置」を選択し、「OK」をクリックしてください。
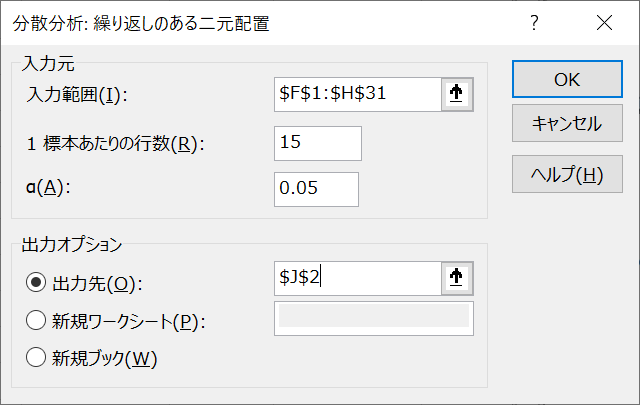
「入力範囲」には列名や行名を含めたデータ全体を指定します。「1標本あたりの行数」には、このデータでは数学と英語でそれぞれ15個のデータがあるため、「15」と入力します。出力先を指定し、最後に「OK」をクリックしましょう。
分散分析の結果が表示されました。
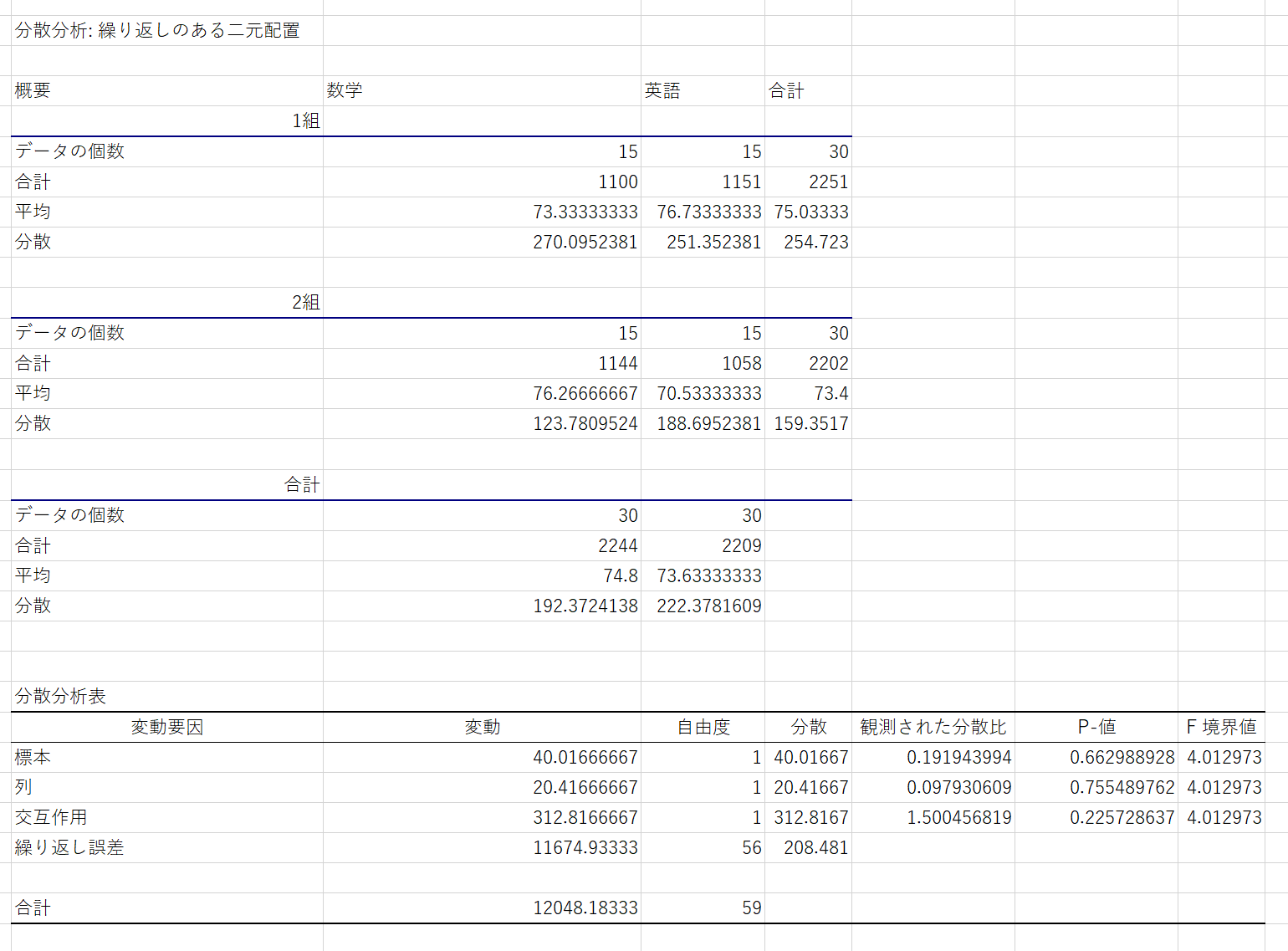
たくさんの値が表示されていますが、まず注目すべきは「P-値」という値です。P-値は「帰無仮説が起こる確率」を意味します。分散分析においての帰無仮説とは「データ群の平均が等しいこと」であり、本データでは「クラス・科目別のテスト点数平均が同じこと」です。
一般的な目安では、このP-値が5%以下であれば帰無仮説を棄却できると考えられています。本データでは、「平均点が等しいという仮説を棄却(否定)できる」ということであり、つまり「平均点の差がある」ということです。
「標本」の横に表示されているP-値は横方向を比較したP-値、つまり本データでは数学と英語の点数を比較したP-値を意味します。0.66=66%であり、5%以上あるため帰無仮説を棄却できません。つまり、平均点の差が認められないということになります。
「列」のP-値は縦方向のP-値、つまり本データでは1組の2組の平均を比較したP-値を意味します。こちらも5%以上になっており、差は認められません。
なお、分析ツールでは要因が3つ以上あるデータの分散分析はできません。
この記事では、エクセルを用いて代表的な統計処理を行う方法をみてきました。ご紹介した統計処理は、いずれもビジネスにおいて有用なものです。
業務上で多くのデータに触れる方は、エクセル上での処理の仕方を身に付けてはいかがでしょうか。














最新情報・キャンペーン情報発信中