ヒストグラムをExcelで作成！分析に有効なグラフの作り方と解釈の仕方を解説

ヒストグラムは日本語で「度数分布図」と呼ばれ、ある集団の個々の数値の分布を視覚化するグラフです。データ数が少なければ、数字だけでも大体の傾向がわかりますが、データ数が多くなると、数字だけで把握することが難しくなります。そこで、ヒストグラムのグラフにすることで、その分布・ばらつきが一目でわかるようになります。

今回は、日常業務でエクセルを多用する筆者が、ヒストグラムの作成方法とグラフの解釈の仕方についてご紹介します。（Excelバージョン：Office2019）

ヒストグラムとは？どんな特徴がある？

連続したデータを区切り、それぞれに対する個数のばらつき具合を示す度数分布。これをグラフとして表現したものが「ヒストグラム」です。横軸は階級、縦軸は度数を表します。

分かりやすいように、年齢で考えていきます。今回は、それぞれを以下のように区切りました。

• 子供：0～14歳
• 成人：15～64歳
• 前期高齢者：65～74歳
• 後期高齢者：75歳以上

度数分布では、区切ったそれぞれの区分を「階級」と呼びます。次に、階級ごとの人口（2015年データ）を見みます。

• 子供：1586万人
• 成人：7592万人
• 前期高齢者：1726万人
• 後期高齢者：1617万人

度数分布では、階級ごとに振り分けられた人数のことを「度数」と呼びます。上記をまとめると、以下の表ができあがります。

階級	度数
0～14歳	1586万
15～64歳	7592万
65～74歳	1726万
75歳以上	1617万

　

上記のことを「度数分布表」と言います。ヒストグラムは、この度数分布表をグラフ化したものです。

ヒストグラムと棒グラフの違い

ヒストグラムは棒グラフに似ていますが、データが示す意味は全く異なります。棒グラフはグラフの一本一本が独立したデータであるのに対し、ヒストグラムが示すのは全データの内訳であり、構成要素です。そのため、ヒストグラムでは、棒の間隔をなくして階段状のグラフにするのが一般的です。

データの分布を調べてヒストグラムで視覚化することで、さまざまな判断材料として役立ちます。例えば、学校で、生徒の体重を5キロごとに刻んだデータでヒストグラムを作ると、体重別の分布がわかり、全国平均と比較した上で「肥満対策を取るべきかどうか」といった視点での判断材料に使えます。
ほかにも、社員の年齢や営業成績の分布をわかりやすく可視化することで、的確な対策を考えることができます。

一方、棒グラフは、それぞれの独立したデータを比較する際に用いられます。たとえば地域別の人口を表したり、支店ごとの売上集計を可視化したりして比べるのに便利です。

なお、ヒストグラムは分布を調べるので、階級（横軸）を連続した順番で並べる必要がありますが、棒グラフについては順番がありません。そもそも、軸に対する決まりがないのも特徴です。ヒストグラムについては、必ず横軸が階級、縦軸を度数にする必要があります。

　

ヒストグラムをエクセルで！2種類の作り方をキャプチャ付きで解説

ヒストグラムの作成はExcelを用いるのが便利です。手法には「FREQUENCY関数で作成した度数分布表からグラフを挿入する方法」と、「Excelのグラフ機能を使う方法」の2つがあります。

基本的には後者を用いるのが簡単ですが、前者についてもぜひ勉強のつもりでチャレンジしてみましょう。

なお、今回は以下のデータを基に解説を行います。

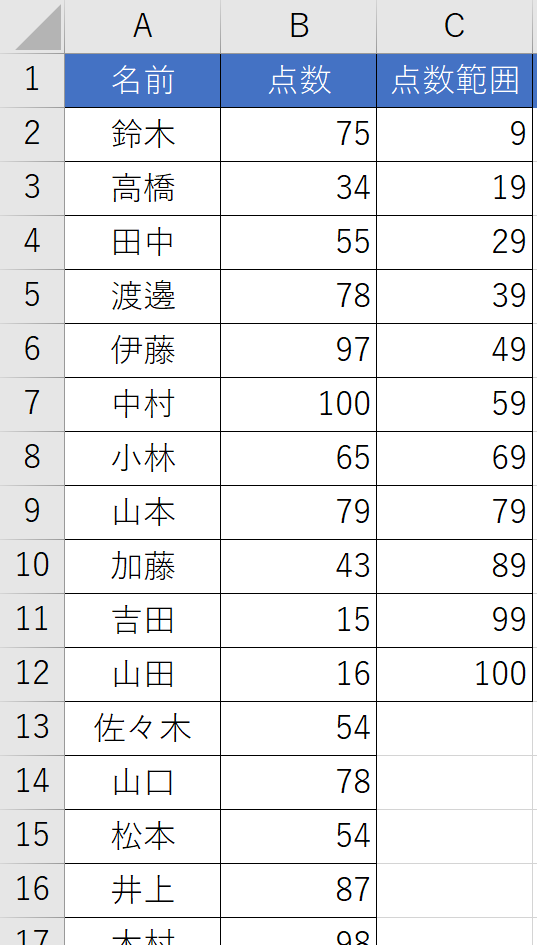
ここでは生徒50人の100点満点のテスト成績を例に取り、A列のA2～A51に生徒の氏名を入力し、B列のB2～B51にそれぞれの点数を入力します。続けて、C列に「点数範囲」を入力します。点数範囲は、10点刻みの11区間としてC2～C12の順に9、19、29…99、100と各範囲の上限の値を入力します。

ヒストグラムの作り方①FREQUENCY関数で度数分布表を作る

まずはExcelのFREQUENCY関数を使って度数分布表を作り、その後グラフにする方法です。比較的手順が多いのですが、度数分布の基本も学べるので、一度試してみてください。

• D列に「人数」欄を作り、11個のセル範囲D2～D12を選択します

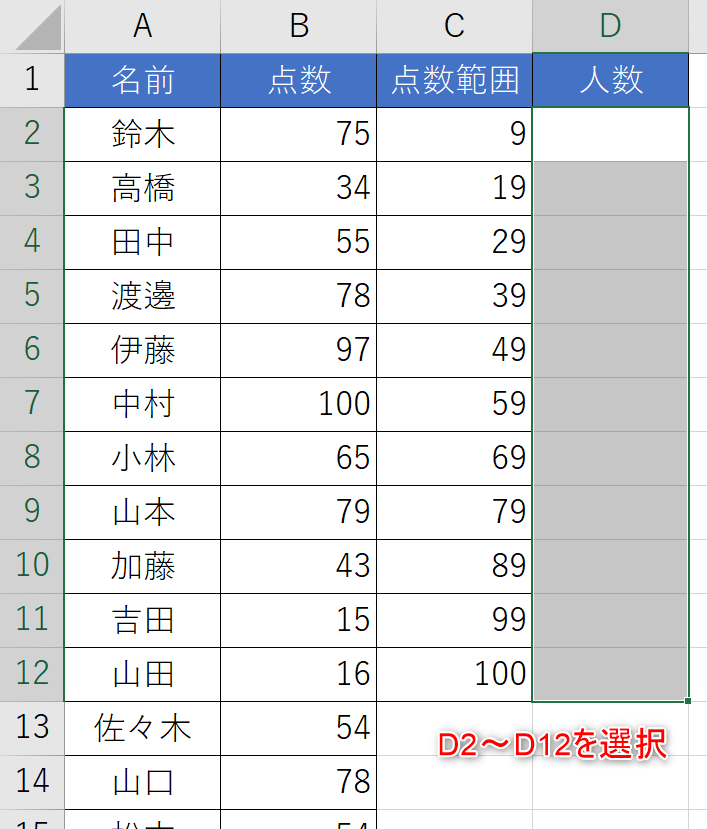
• ［数式］タブ内の［関数の挿入］ボタンを押します。

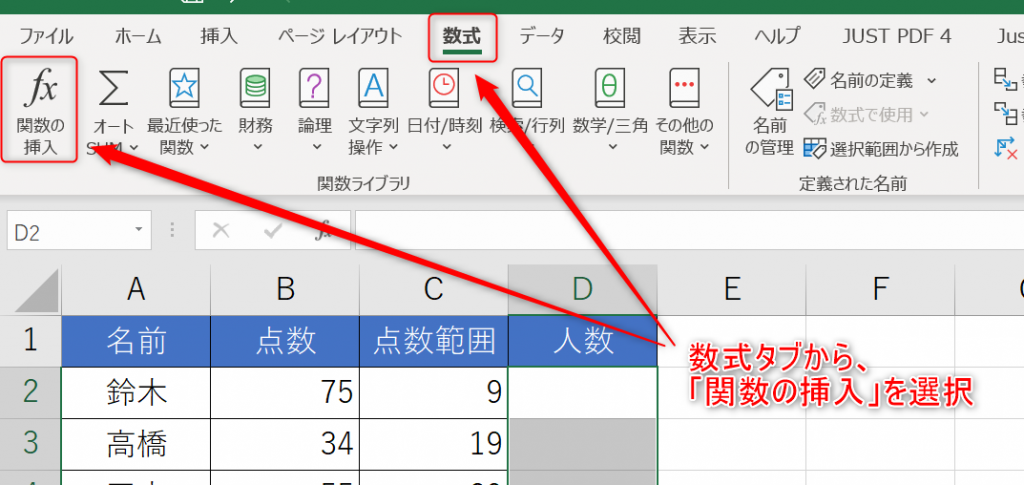
• 検索バーに「FREQUENCY」（小文字でも構いません）と入力して検索します。「FREQUENCY」がハイライトされていることを確認して［OK］ボタンを押します。

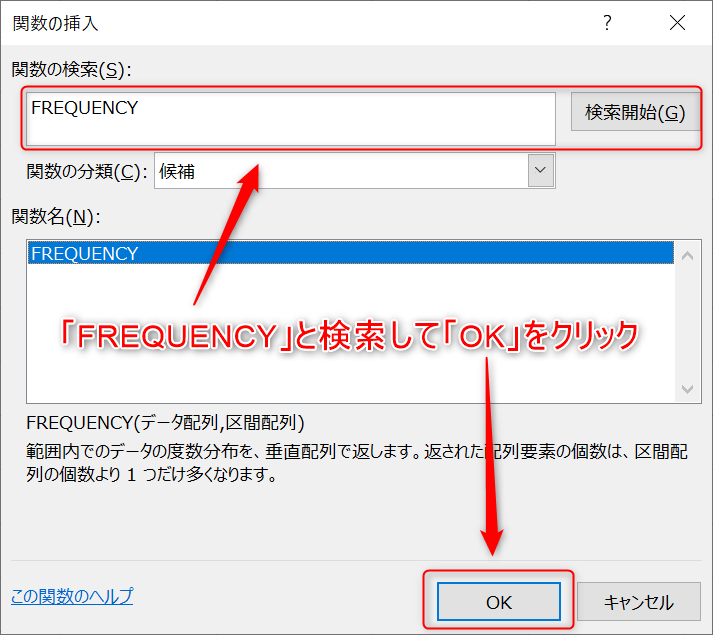
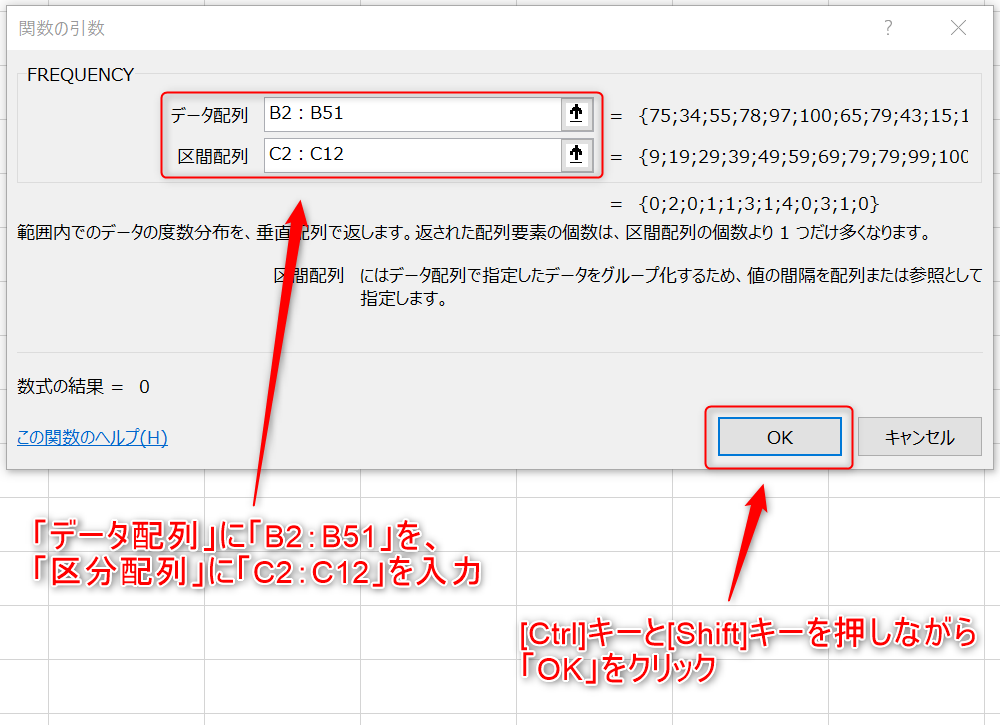
• 関数の引数ウィザードで、［データ配列］の欄にデータ範囲（この場合はB2：B51）を選択、［区間配列］にはC2：C12を入れ、［Ctrl］キーと［Shift］キーを同時に押しながら［OK］ボタンをクリックします。
  この同時押しは、絶対参照で選択範囲に全て同じ式や値を入力するときに使います。ここで［OK］だけをクリックすると1つのセルにしか式が入力されません。しかも、相対参照のためセルのコピーだけでは参照範囲が変わってしまいます。

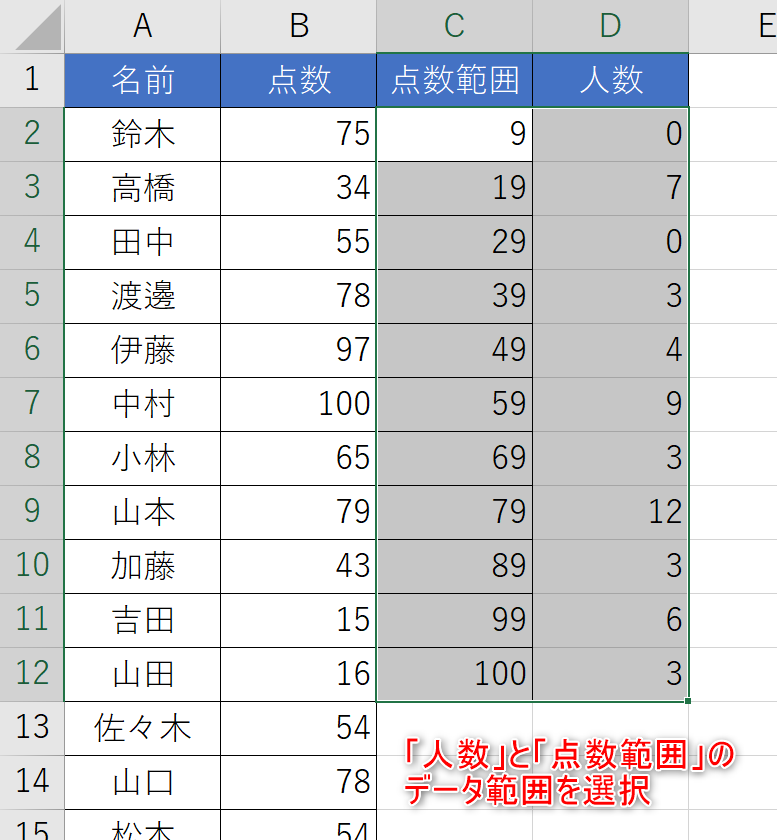
• 「人数」と「点数範囲」のデータ範囲を選択する。

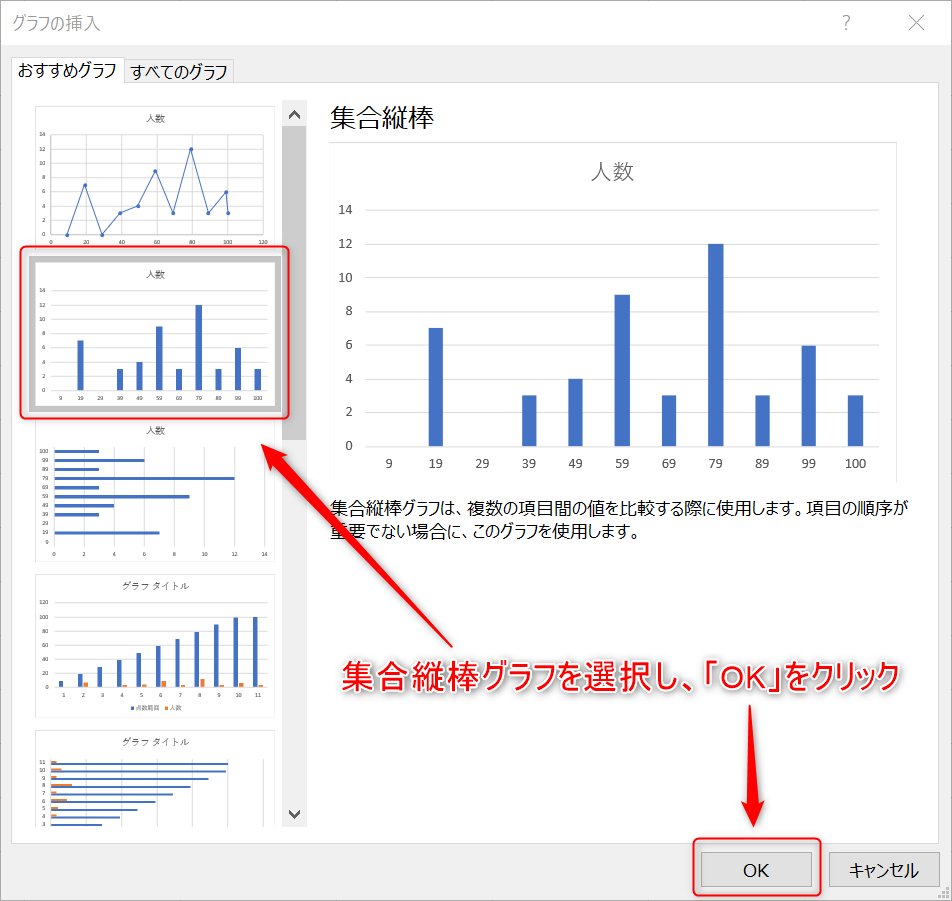
• ［挿入］タブ内の「おすすめグラフ」から集合縦棒を選びます。

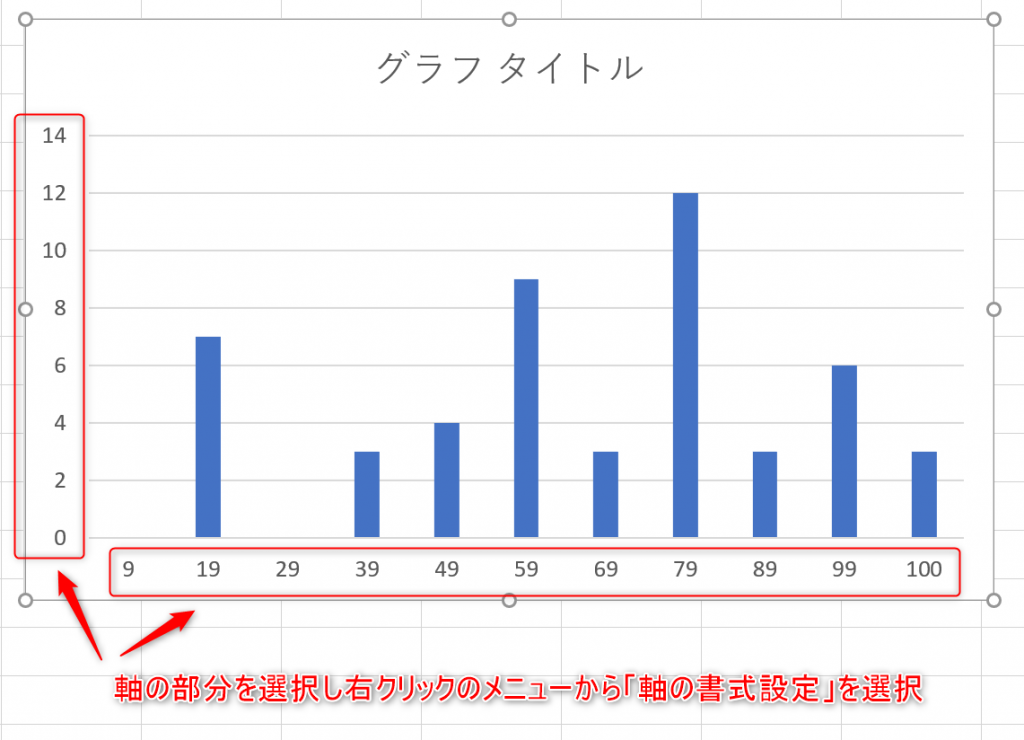
• 縦軸と横軸を変更したい場合は、軸の部分を選択し右クリックのメニューから「軸の書式設定」を選び、整えてください。

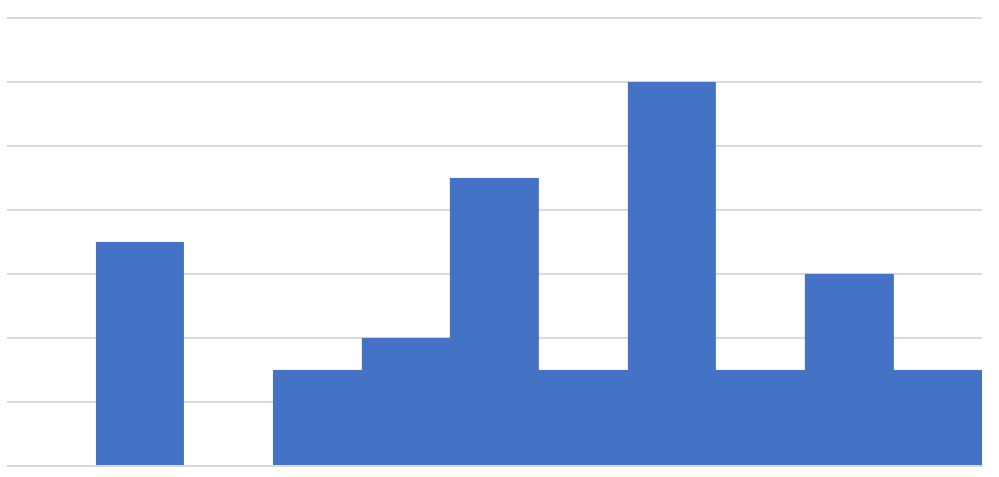
• グラフの棒の部分を選択し右クリックのメニューから「データ系列の書式設定」を選びます。「要素の間隔」を0％にすると、縦棒の間隔があいていないヒストグラムが完成します。

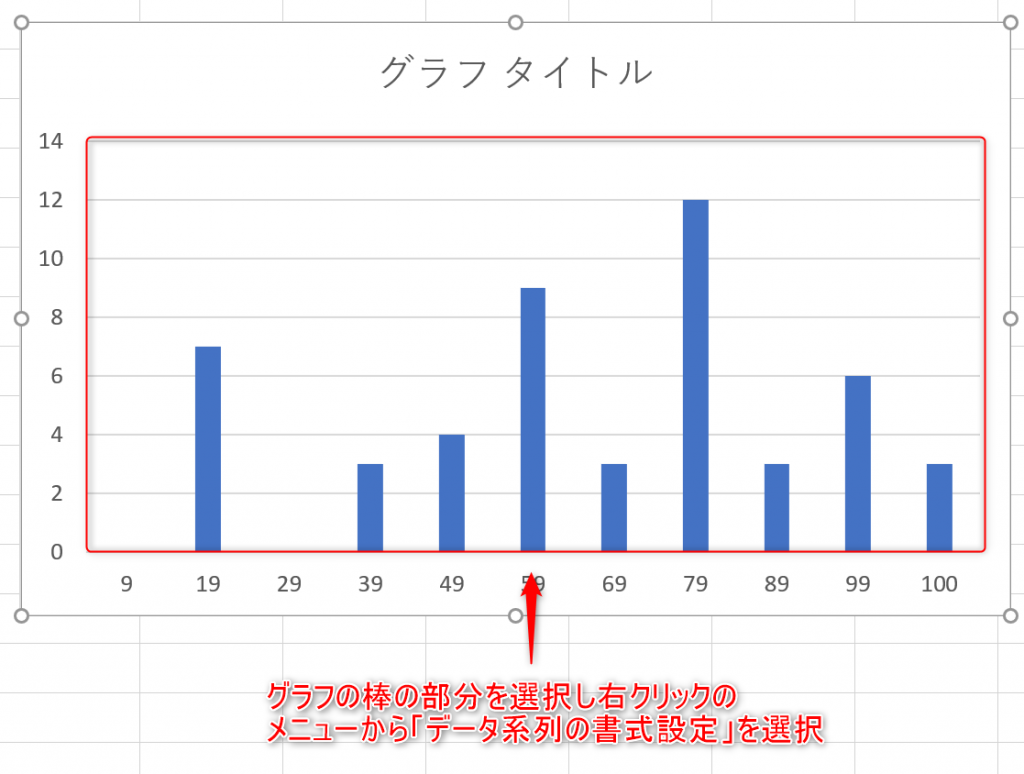
• ヒストグラムが完成します。

　

ヒストグラムの作り方②グラフの挿入機能を使う

Excelのバージョン2016以降には、ヒストグラムを直接挿入できるグラフ機能があります。FREQUENCY関数を使ったものより手早く簡単にできるので、実務の際にはこちらがおすすめです。

• まずは①点数の範囲を選択し、②挿入タブから③ヒストグラムを選択します。

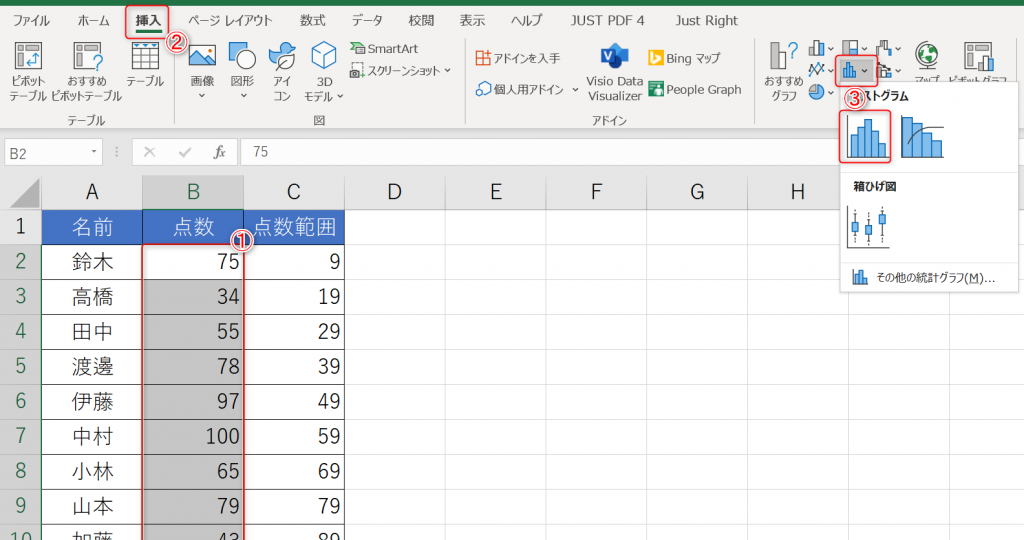
• ヒストグラムが作成されます。ただし、階級は自動で設定されているので、任意の設定を行います。横軸部分を右クリックし、メニューから「軸の書式設定」を選択します。

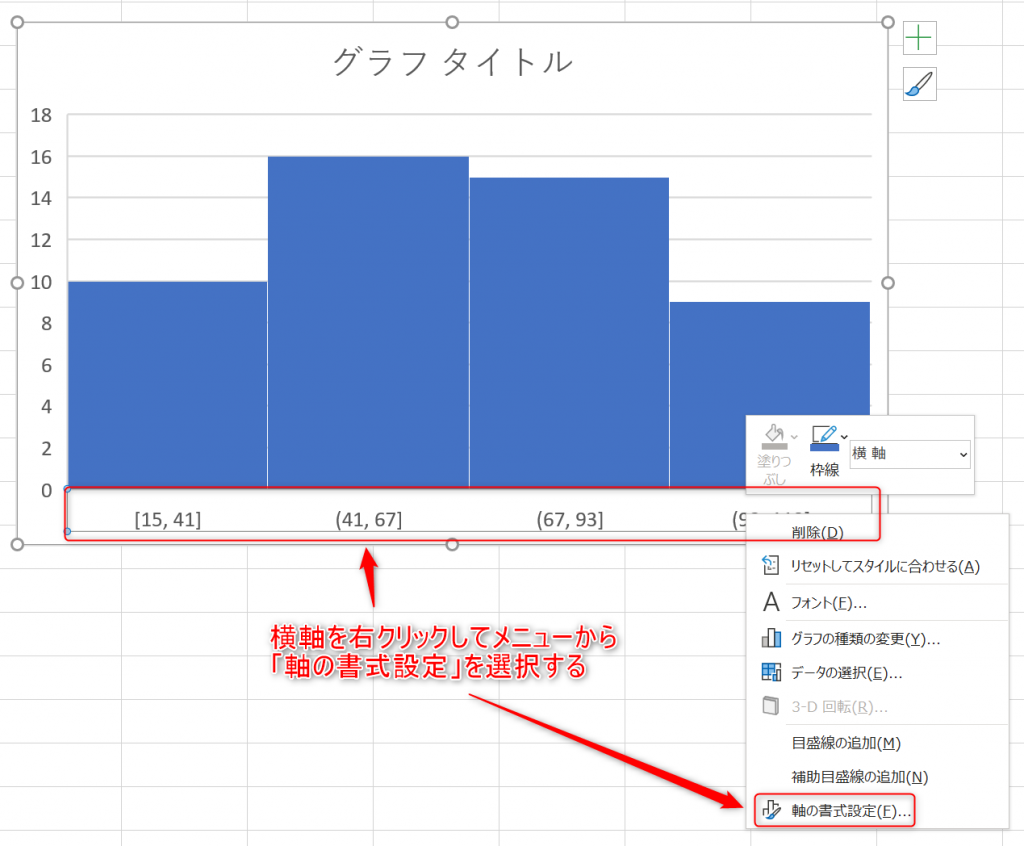
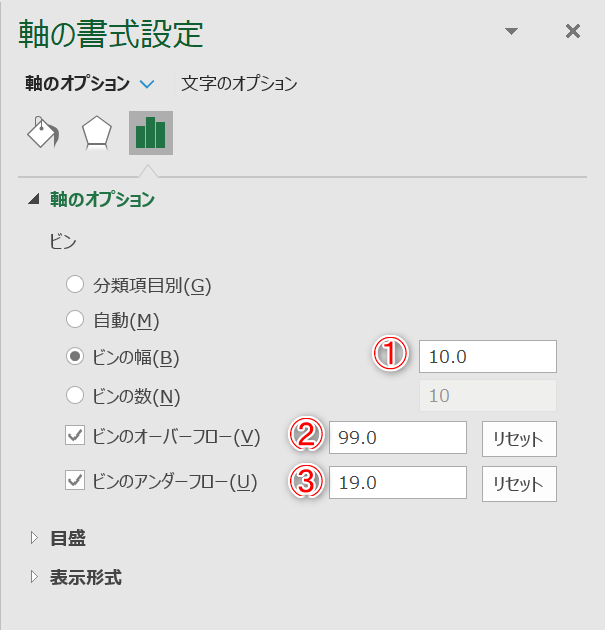
• まずは①ピンの幅で階級の区切り単位を設定します。次に②ピンのオーバーフローと③ピンのアンダーフローにチェックを入れ、それぞれに数値を入力します。ピンのオーバーフローは最後の区間の下限値を、ピンのアンダーフローは最初の区間の下限値を表します。

• ヒストグラムが完成しました。

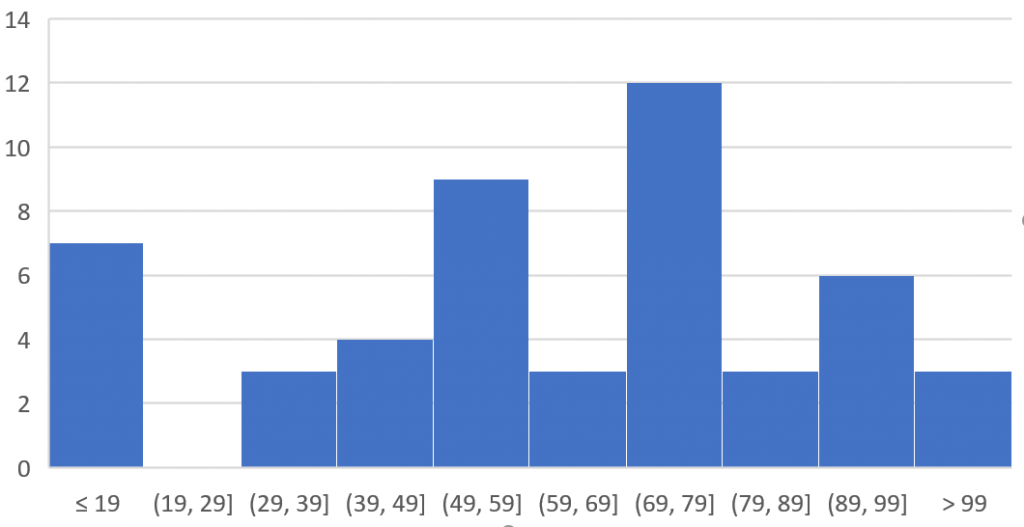
なお、Excelのバージョン2016以前ではヒストグラムの直接挿入は行えません。この場合は、FREQUENCY関数を使うか、アドインのインストールが必要ですので、ご注意ください。

　

ヒストグラムの種類とグラフから分析できること

ヒストグラムが完成した後は、その形から分析を行います。この際には、グラフの形状からさまざまなことを予測できます。

また、元のデータがない状態であっても、ヒストグラムがあればおおよその平均値や中央値、最頻値、標準偏差が求められます。これも、分析に際には役立つはずです。

ヒストグラムの種類

ヒストグラムの形には、いくつかの種類があります。それぞれの分析方法や特徴について解説します。

左右対称型（一般型）

代表的なのは中央が最も高い山型で左右の高さも対称に近い形です。中心にいくほど分布が高くなり、安定したデータといえます。例えば、部品の品質管理では、中央が飛び抜けて高く、左右に広がりが狭いのが理想的な形です。そうでない場合は、製造工程に何らかの問題が生じている可能性があります。

ふた山型

山が2つ、3つあるヒストグラムの代表的な例は、日本の人口分布図です。まさに、山が2つある形ですが、これはベビーブームとその子供、孫が多いことを意味しています。その他のデータでこの形になる場合は、異なるデータが2つ以上入っている可能性があるため元のデータを一度確認する必要があります。

すそ引き型

片側に大きく傾斜する形も異種データが含まれる可能性があり、データを点検したほうが良いでしょう。サンプル数が少なすぎて分布の特徴が出ていないかもしれません。例えば、テスト成績でこのような形になる場合は、出題が簡単もしくは難しすぎて、生徒の実力差を十分に反映していないという可能性もあります。

歯抜け型（くし歯型）

階級ごとに度数が凸凹な状態のヒストグラムです。階級ごとの幅が狭かったり、データが少なかったりする場合に多く見られます。誤ったグラフではないものの、分析がしにくいようであれば階級の幅を広げたり、データを多くしたりすることで、他の形状に近づく場合があります。

絶壁型

いずれかの階級へ大きく度数が偏っている形状です。極端なスクリーニングが行われていたり、そもそも測定に誤りがあったりする場合に多く見られます。

離れ小島型

中央値と離れた側に小さな山がある形状です。絶壁型同様に、データの選別や、計測ミスが疑われます。ただし、離れた山がある程度の大きさの場合は、イレギュラーな要因が含まれている可能性もあります。

高原型

各階級の度数に差がない状態で現れる形状です。異なる平均値の分布が混ざってしまっている場合があるので、階級分けなどを見直してみてください。

ヒストグラムから求められる値

ヒストグラムのみのデータからも、平均値や中央値などが求められます。階級で分けられているため多少の誤差はあるものの、分析に役立ちます。

平均値

各階級の中央の値である階級値を求めた上で、各度数のデータを以下の数式に入れます。

（階級値×度数）の合計÷度数の合計
なお、階級値は以下の数式で求められます。
（階級の最大値＋階級の最小値）÷2

中央値

中央値とは、順番にデータを並べた際に中央にある値のことです。たとえばデータが100ある場合は、その50番目と51番目の階級値を求めます。それぞれを合計し、2で割ることで中央値が算出されます。
（中央の値1つ目＋中央の値2つ目）÷2

最頻値

最頻値とは、「もっとも度数が高い階級における階級値」です。ヒストグラムのなかでもっとも度数が高い数値が最頻値となります。

標準偏差

標準偏差を求めるためには、以下の手順を踏みます。

• 各階級の階級値と平均値を求める
• 階級値から平均値を引いて偏差を求める
• 偏差の2乗に度数をかける
• 前手順で求めた各階級の合計を、データの合計で割る
• 前手順で求めた値を正の平方根で計算する

標準偏差を求めたい場合には「標準偏差をエクセルで求める方法と完璧なグラフの作り方！」も参考にしてみてください。

　

【応用編】累積グラフなどを用いたヒストグラムの作り方

次に、ヒストグラムと他のグラフを組み合わせた応用的なテクニックをご紹介します。

累積グラフ

累積相対度数（その階級までに含まれているデータの割合）はヒストグラムと合わせて用いられることの多い分析方法です。今回の場合であれば、その点数以下の生徒が何割いるか？　といったことを表せます。

• まずは「①FREQUENCY関数で度数分布表を作る」の手順で度数分布表を作ります。
• 相対度数と累積相対度数をグラフに追加します。
• ①相対度数：各階級の度数を全体の件数で割った値（今回の場合は50）
• ②累積相対度数：相対度数をはじめの階級から順に足し上げた値

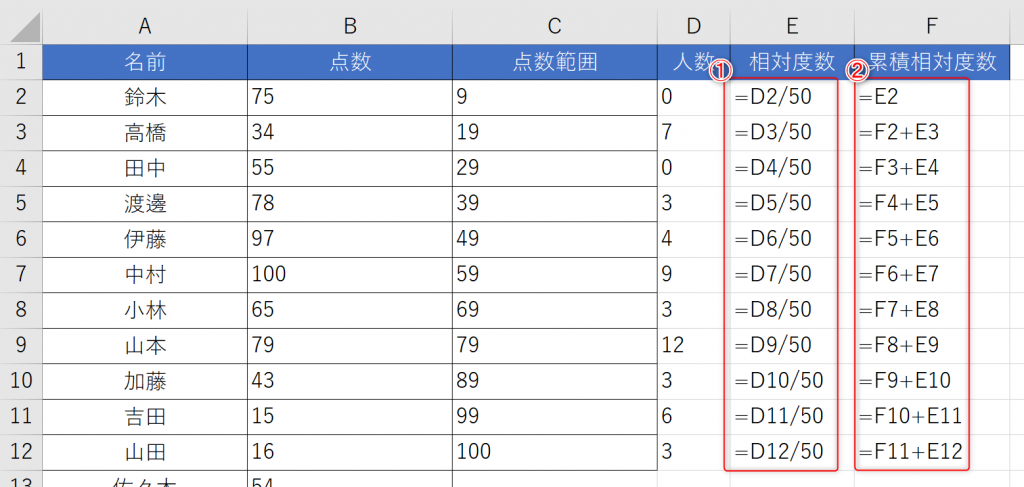
※上記では分かりやすいようにE・F列の数式を表示しています

• 人数と累積相対度数のデータを選択し、「挿入タブ」内の「おすすめグラフ」をクリックします。

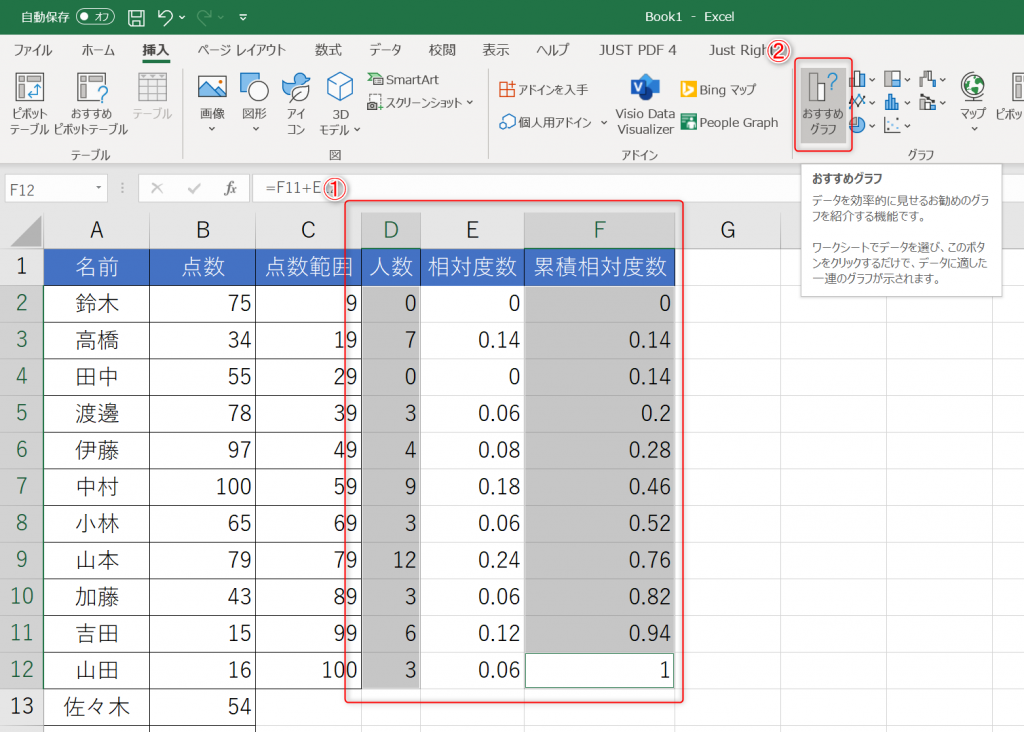
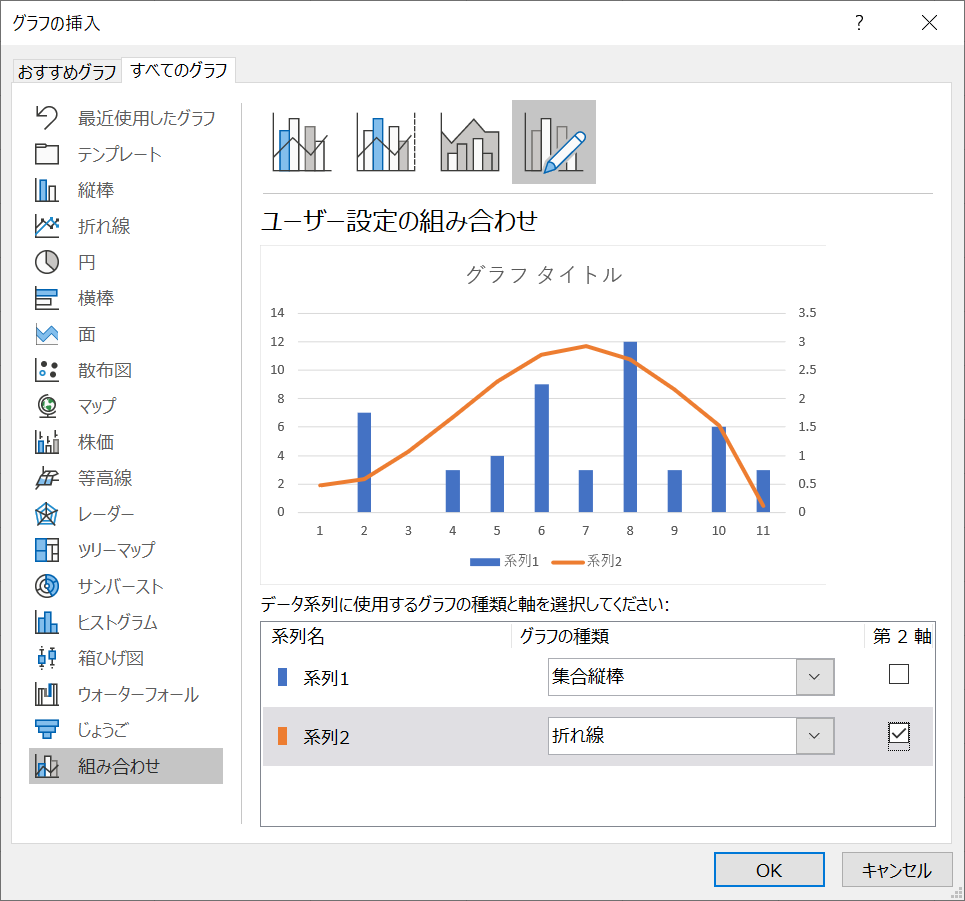
• グラフ挿入ウィンドウの①「すべてのタブ」タブを選択し、左メニューのなかから②「組み合わせ」を選択してください。そこでグラフに関する設定を行います。
  系列1は人数なのでそのまま、系列2が累積相対度数なので、第2軸のチェックを入れます。

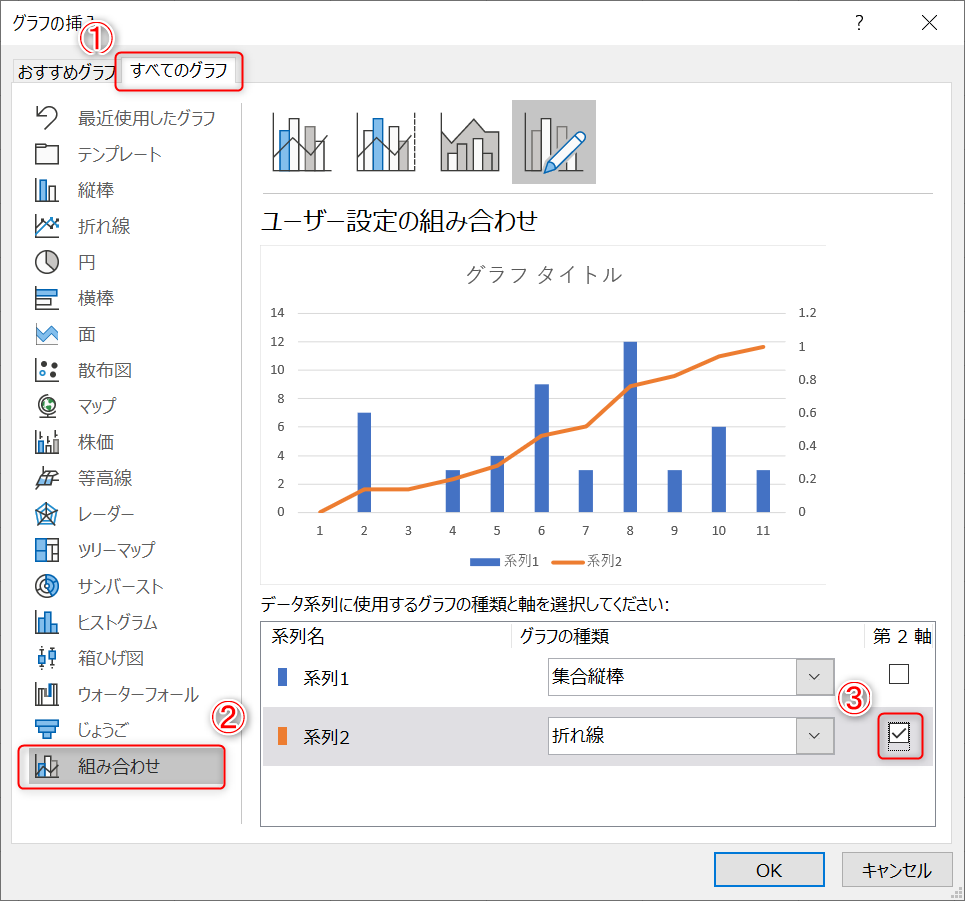
• 「OK」を押すとグラフが作られます。「①FREQUENCY関数で度数分布表を作る」と同じ手順で棒グラフの「要素の間隔」を0%に設定すれば完成です。

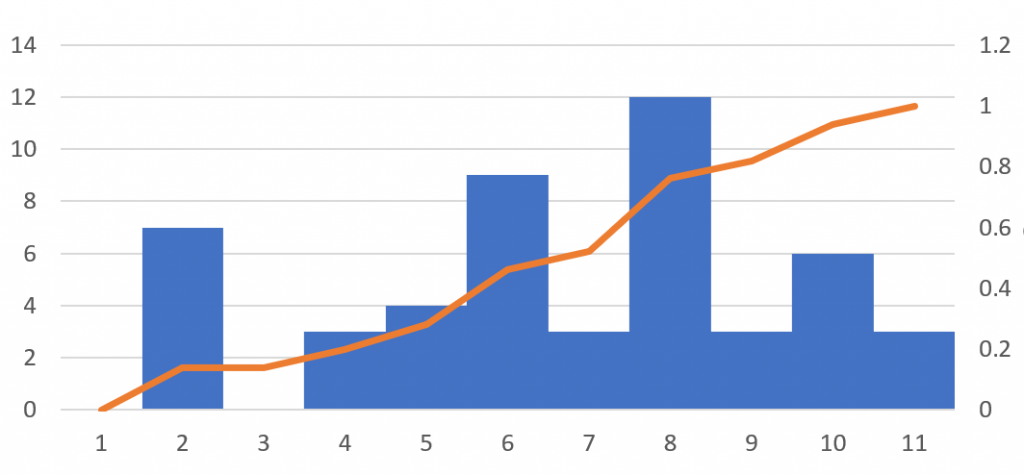
正規分布曲線

次に、ヒストグラムと確率分布を表す正規分布曲線を重ねてみましょう。やや手順は複雑ですが、以下の手順で表現できます。

• まずは「①FREQUENCY関数で度数分布表を作る」の手順で度数分布表を作ります。
• データの平均（AVERAGE関数）と標準偏差（STDEV.S関数）を関数で求めます。

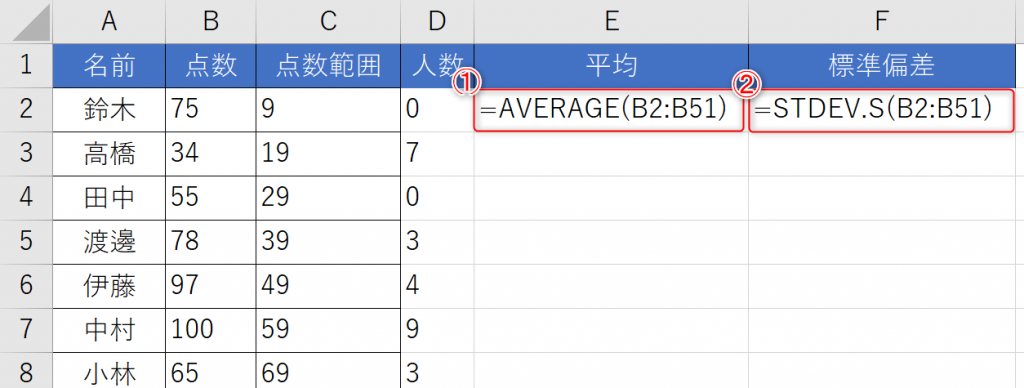
※上記では分かりやすいようにE・F列の数式を表示しています

• 各階級における点数範囲の正規分布をNORMDIST関数で計算します。

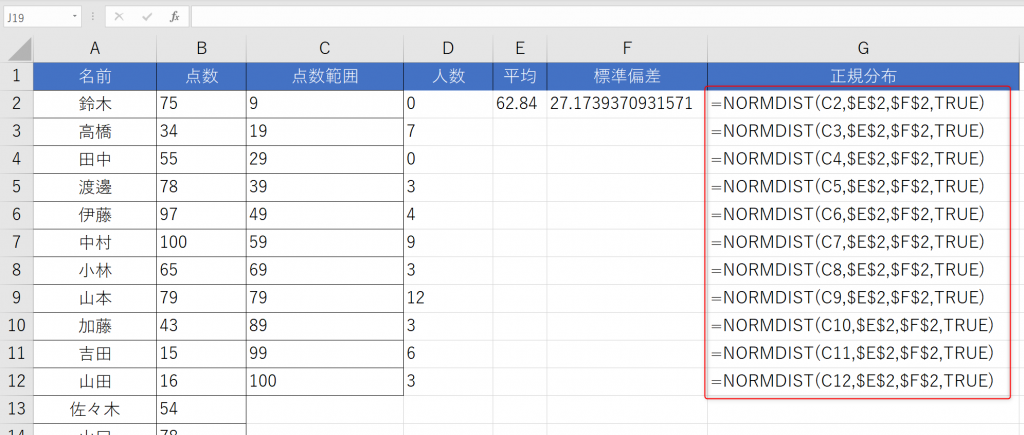
※上記では分かりやすいようにG列の数式を表示しています

• 正規分布の1つ前の階級までを引いた正規分布図を作ります。

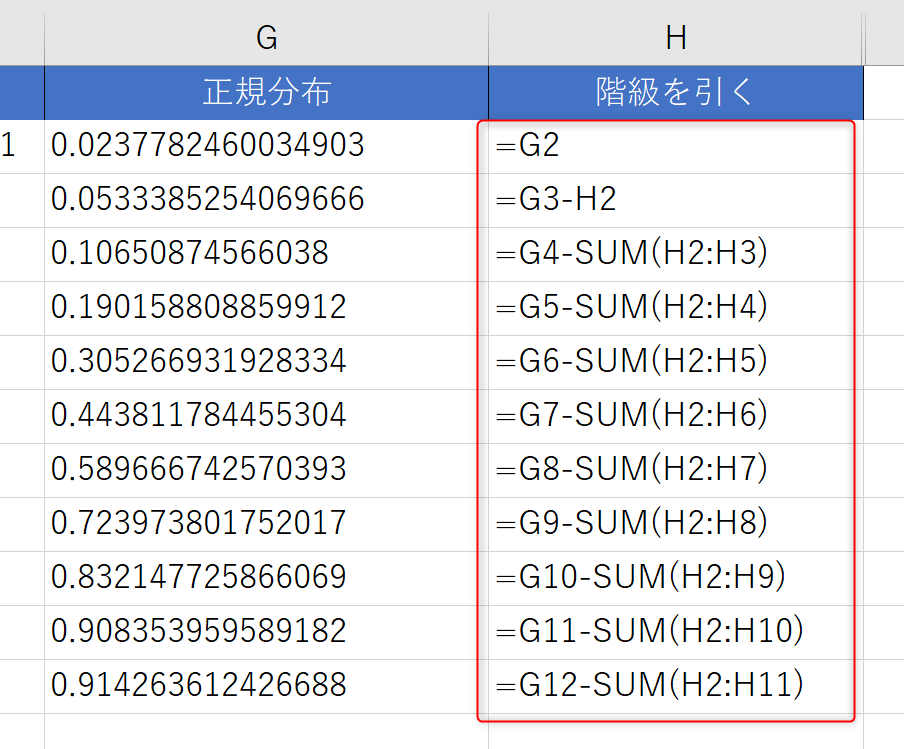
※上記では分かりやすいようにH列の数式を表示しています

• このままの数値だとグラフにした際に点数（度数）に対して小さすぎてしまうため、今回はすべてに20をかけて調整をしました。

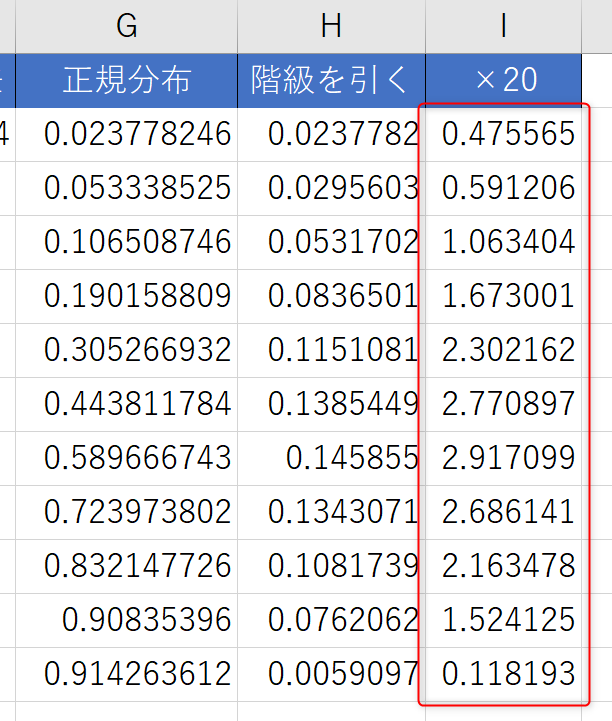
• D列（人数）とI列（×20）のデータを選択し、累計グラフのときと同様に組み合わせグラフ作成します。

• 「OK」を押すとグラフが作られます。「①FREQUENCY関数で度数分布表を作る」と同じ手順で棒グラフの「要素の間隔」を0%に設定すれば完成です。

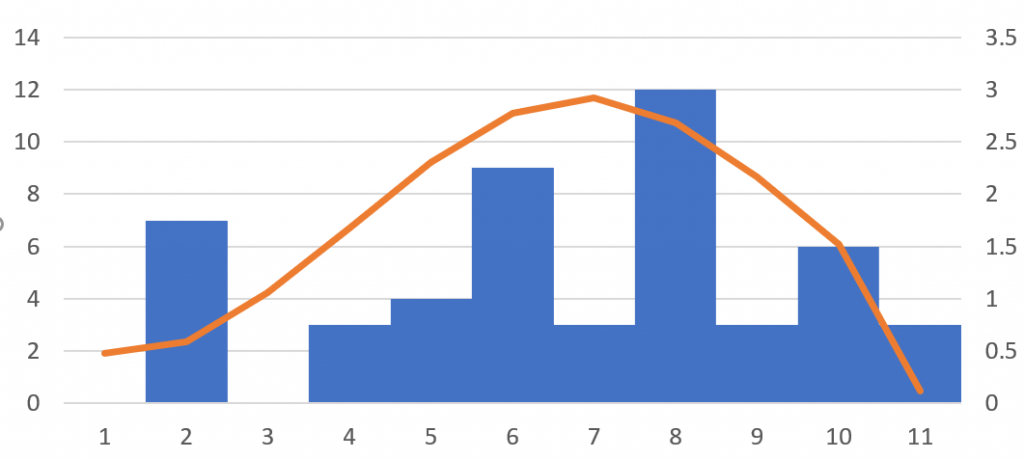
ヒストグラムを適切に使いこなせるようになろう！

今回はヒストグラムの2つの作成方法や分析、応用方法などをご紹介しました。ばらつきを視覚化して表現するには、ヒストグラムが最適です。作成のコツをつかめば、よりわかりやすい分析レポートや資料作成に活かすことができます。

エクセルは実務で使える実践的な知識を身に付けることがとても大切です。
下記のUdemy講座ではIF関数をもとにした6つの実務事例を解説しており、なんと無料で学ぶことができます。

＼完全無料！／
【Excel】IF関数を使いこなす！実務事例から学ぶ本格スキル習得講座（事例6選）

評価：★★★★★
コメント： IF関数に強い苦手意識を持っていましたが、無料でこんなに分かりやすく学べて感謝しています。

評価：★★★★★
コメント： ある程度分かっているつもりでしたが、条件付き書式も１事例あって、知らない内容が含まれていたため、勉強になりました。

これを機に実務に使える実践的なExcelの知識を身につけましょう！